
| f(x) |
| g(x) |
| A、(-∞,0] |
| B、[0,+∞) |
| C、(-∞,0) |
| D、(0,+∞) |
| f(x) |
| g(x) |
| f(x) |
| g(x) |
| f′(x)g(x)-f(x)g′(x) |
| g2(x) |
| f(x) |
| g(x) |
| f(x) |
| g(x) |
| f(0) |
| g(0) |
| f(x) |
| g(x) |
| f(x) |
| g(x) |


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
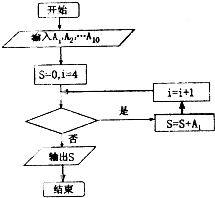 如表是我市抽查部分高中学生的身高统计表,从左到右的各组表示的学生人数依次记为A1,A2,…,A10(如A2表示身高[150,155)内的人数),如图是统计表中身高在一定范围内的学生人数的程序框图,如果要统计身高在160-180cm(含160cm不含180cm)的学生人数,那么空白的判断框内应填写的条件是( )
如表是我市抽查部分高中学生的身高统计表,从左到右的各组表示的学生人数依次记为A1,A2,…,A10(如A2表示身高[150,155)内的人数),如图是统计表中身高在一定范围内的学生人数的程序框图,如果要统计身高在160-180cm(含160cm不含180cm)的学生人数,那么空白的判断框内应填写的条件是( )| 分组 | [145,150) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) | [190,195) |
| 人数 | 146 | 251 | 352 | 510 | 618 | 522 | 388 | 293 | 108 | 89 |
| A、i<6? | B、i<7? |
| C、i<8? | D、i<9? |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com