
分析 (1)直线y=mx+1过定点(0,1),且在椭圆的内部,可得结论;
(2)直线y=mx+1过定点(0,1),设A(x1,y1),B(x2,y2),则OP的中点M为($\frac{x}{2}$,$\frac{y}{2}$),且有2x12+y12=2,2x22+y22=2,由此能求出点P的轨迹方程.
(3)假设存在直线l,使OAPB为矩形.由于OA⊥OB,则有x1x2+y1y2=0,运用韦达定理及点在直线上满足直线方程,化简整理得到的方程,解出m,注意检验判别式是否大于0.
解答 (1)证明:直线y=mx+1过定点(0,1),且在椭圆的内部,
∴椭圆C:ax2+y2=2(a>0)与直线L:y=mx+1总有两个交点.
(2)解:设A(x1,y1),B(x2,y2),
则OP的中点M为($\frac{x}{2}$,$\frac{y}{2}$),
且有2x12+y12=2,2x22+y22=2,
以上两式相减,得kAB•kOP=-2,
∴$\frac{\frac{y}{2}-1}{\frac{x}{2}}•\frac{y}{x}$=-2,
∴2x2+y2-2y=0,
点P的轨迹方程为2x2+(y-1)2=1(除去原点).
(3)解:由直线与椭圆联立,得(a+m2)x2+2mx-1=0,
∴x1+x2=-$\frac{2m}{a+{m}^{2}}$,x1x2=-$\frac{1}{a+{m}^{2}}$,
y1y2=(mx1+1)(mx2+1)=m2x1x2+m(x1+x2)+1=$\frac{a-2{m}^{2}}{a+{m}^{2}}$,
由于OA⊥OB,则有x1x2+y1y2=0,即为-$\frac{1}{a+{m}^{2}}$+$\frac{a-2{m}^{2}}{a+{m}^{2}}$=0,
解得,a=2m2-1.
检验:判别式△>0,成立.
故存在直线l:y=±$\sqrt{\frac{a+1}{2}}$(x+1),使OAPB为矩形.
点评 本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
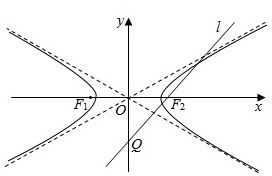 如图,双曲线Γ:$\frac{{x}^{2}}{3}$-y2=1的左、右焦点分别为F1,F2,过F2作直线l交y轴于点Q.
如图,双曲线Γ:$\frac{{x}^{2}}{3}$-y2=1的左、右焦点分别为F1,F2,过F2作直线l交y轴于点Q.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinα=$\frac{3}{5}$ | B. | cosα=-$\frac{4}{5}$ | C. | tanα=-$\frac{3}{4}$ | D. | tanα=-$\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com