
【题目】已知f(x)=﹣4x2+4ax﹣4a﹣a2在区间[0,1]内有一最大值﹣5,求a的值.
【答案】解:∵f(x)=﹣4x2+4ax﹣4a﹣a2=﹣4(x﹣ ![]() )2﹣4a,对称轴为x=
)2﹣4a,对称轴为x= ![]() ,
,
当a<0时, ![]() <0,∴f(x)在区间[0,1]上是减函数,
<0,∴f(x)在区间[0,1]上是减函数,
它的最大值为f(0)=﹣a2﹣4a=﹣5,
∴a=﹣5,或a=1(不合题意,舍去),
∴a=﹣5;
当a=0时,f(x)=﹣4x2 , 不合题意,舍去;
当0<a<2时,0< ![]() <1,f(x)在区间[0,1]上的最大值是f(
<1,f(x)在区间[0,1]上的最大值是f( ![]() )=﹣4a=﹣5,
)=﹣4a=﹣5,
∴a= ![]() ;
;
当a≥2时, ![]() ≥1,f(x)在区间[0,1]上是增函数,
≥1,f(x)在区间[0,1]上是增函数,
它的最大值为f(1)=﹣4+4a﹣4a﹣a2=﹣5,
∴a=±1,(不合题意,舍去);
综上,a的值是 ![]() 或﹣5
或﹣5
【解析】先求对称轴,比较对称轴和区间的关系,利用二次函数的图象与性质来解答本题.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能正确解答此题.
上递减才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】设集合M是R的子集,如果点x0∈R满足:a>0,x∈M,0<|x﹣x0|<a,称x0为集合M的聚点.则下列集合中以1为聚点的有( ) ① ![]() ;
;
② ![]() ;
;
③Z;
④{y|y=2x}.
A.①④
B.②③
C.①②
D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017衡阳第二次联考】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)如果对于任意的![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,
, ![]() ,过点
,过点![]() 作函数
作函数![]() 的图象的所有切线,令各切点的横坐标按从小到大构成数列
的图象的所有切线,令各切点的横坐标按从小到大构成数列![]() ,求数列
,求数列![]() 的所有项之和的值.
的所有项之和的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某活动小组为了估计装有5个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇兑起来后,摸到红球次数为6000次.
(1)估计从袋中任意摸出一个球,恰好是红球的概率是 ;
(2)请你估计袋中红球接近 个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直角坐标平面内的两个点P和Q满足条件:①P和Q都在函数y=f(x)的图象上;②P和Q关于原点对称,则称点对[P,Q]是函数y=f(x)的一对“友好点对”([P,Q]与[Q,P]看作同一对“友好点对”).已知函数 ![]() ,则此函数的“友好点对”有( )
,则此函数的“友好点对”有( )
A.0对
B.1对
C.2对
D.3对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的某产品产量与单位成本的资料如表所示:
产量x千件 | 2 | 4 | 5 | 6 | 8 |
单位成本y元/件 | 30 | 40 | 60 | 50 | 70 |
请画出散点图并从图中判断产品产量与单位成本成什么样的关系?
查看答案和解析>>
科目:高中数学 来源: 题型:
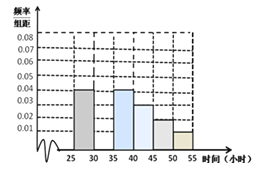
【题目】教育部,体育总局和共青团中央号召全国各级各类学校要广泛,深入地开展全国亿万大,中学生阳光体育运动,为此,某校学生会对高二年级2014年9月与10月这两个月内参加体育运动的情况进行统计,随机抽取了100名学生作为样本,得到这100名学生在该月参加体育运动总时间的小时数,根据此数据作出了如下的频数和频率的统计表和 频率分布直方图:
(I)求a,p的值,并补全频率分布直方图;
(Ⅱ)根据上述数据和直方图,试估计运动时间在[25,55]小时的学生体育运动的平均时间;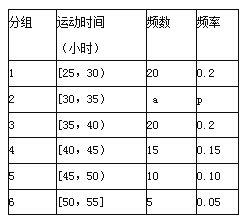
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦点在x正半轴上,顶点为坐标系原点的抛物线过点A(1,﹣2).
(1)求抛物线的标准方程;
(2)过抛物线的焦点F的直线l与抛物线交于两点M、N,且△MNO(O为原点)的面积为2 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com