
����Ŀ������лƺ�̲��ij��2010����2016���˾������루��λ����Ԫ�����������±���
��� | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
��ݴ���x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
�˾�������y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
������y����x�����Իع鷽�̣�
�������ã����еĻع鷽�̣�����2010����2016��ô��˾�������ı仯�������Ԥ��ô�2017���˾������룮
�����ع�ֱ�ߵ�б�ʺͽؾ����С�˷����ƹ�ʽ�ֱ�Ϊ�� ![]() =
= 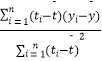 ��
�� ![]() =
= ![]() ��
�� ![]() ��
��
���𰸡��⣺����������������������ƽ���� ![]() =
= ![]() =4��
=4�� ![]() =
= ![]() =4.3��
=4.3��
�� ![]() ��xi��
��xi�� ![]() ����yi��
����yi�� ![]() ��=����3��������1.4��+����2��������1��+����1��������0.7��+0+1��0.5+2��0.9+3��1.6=14
��=����3��������1.4��+����2��������1��+����1��������0.7��+0+1��0.5+2��0.9+3��1.6=14
![]() ��xi��
��xi�� ![]() ��2=9+4+4+0+1+4+9=28��
��2=9+4+4+0+1+4+9=28��
�� ![]() =
= 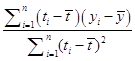 =
= ![]()
�� ![]() =4.3��
=4.3�� ![]() ��4=2.3��
��4=2.3��
��y����x�����Իع鷽��Ϊ��y= ![]() x+2.3��
x+2.3��
�����ɣ��ɵ����Իع鷽��Ϊy= ![]() x+2.3��
x+2.3��
2017���˾������룬��x=8���ɵ�y= ![]() ����Ԫ����
����Ԫ����
��Ԥ��ô�2017���˾�������Ϊ6.3��Ԫ
���������������ù�ʽ��� ![]() ��
�� ![]() �����ɵó����ۣ��������ã������Իع鷽�̣�����x=8���ɣ�
�����ɵó����ۣ��������ã������Իع鷽�̣�����x=8���ɣ�


 ���100��1�ž�ϵ�д�
���100��1�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������䣨��2��a����a��0������ȡһ����m��������f��x��=3x+m��3 ![]() ������[1��+�ޣ������ĸ��ʲ�С��
������[1��+�ޣ������ĸ��ʲ�С�� ![]() ����ʵ��a��ȡ����С�����ǣ� ��
����ʵ��a��ȡ����С�����ǣ� ��
A.1
B.3
C.5
D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������{an}��ǰn���ΪSn �� ��a1=2��an+1=2Sn+2��
��1��������{an}��ͨ�ʽ��
��2��������{bn}�ĸ����Ϊ��������bn�� ![]() ��
�� ![]() �ĵȱ������bn��ǰn���Tn ��
�ĵȱ������bn��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1���жϺ���![]() ����ż�ԣ�
����ż�ԣ�
��2���жϲ�֤��![]() )��
)��![]() ���ϵĵ����ԣ�
���ϵĵ����ԣ�
��3����![]() ������
������![]() ���������
���������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������![]() �У�����
�У�����![]() Ϊ���Σ�
Ϊ���Σ� ![]() ƽ��
ƽ��![]() ��
�� ![]() ����
����![]() Ϊ
Ϊ![]() ���е㣮
���е㣮
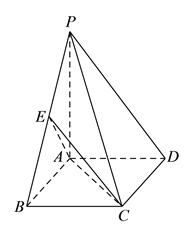
��![]() ����֤��
����֤�� ![]() ƽ��
ƽ��![]() ��
��
��![]() ����֤��ƽ��
����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ��������ε�����P��ABCD�У���ABC=60����PA=AC=a��PB=PD= ![]() ����E��PD���е�.
����E��PD���е�.
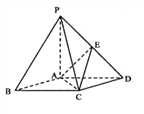
������֤��PA��ƽ��ABCD��
����������E��AC��D�Ĵ�С��
�������P��ƽ��EAC�ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ�����100���ڵļ۸�f(t)��ʱ��t�ĺ�����ϵʽ��

������g(t)��ʱ��t�ĺ�����ϵʽ��g(t)����![]() ��
��![]() (0��t��100)����������Ʒ�������۶�����ֵ��
(0��t��100)����������Ʒ�������۶�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}������a1=1����an+1= ![]() ��n��N*����
��n��N*����
��1��֤��������{ ![]() }�ǵȲ����У���������{an}��ͨ�ʽ��
}�ǵȲ����У���������{an}��ͨ�ʽ��
��2����bn=anan+1 �� ������{bn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������P��ABCD�У�����ABCD�Ǿ��Σ���AD=2��AB=1��PA��ƽ��ABCD��E��F�ֱ����߶�AB��BC���е㣮 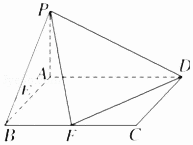
��1��֤����PF��FD��
��2����PA=1�����E��ƽ��PFD�ľ��룮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com