
设集合A={(x,y)|y=2x-1,x∈N*},B={(x,y)|y=ax2-ax+a,x∈N*},问是否存在非零整数a,使A∩B≠∅?若存在,请求出a的值;若不存在,说明理由.
科目:高中数学 来源: 题型:
对于命题:若O是线段AB上一点,则有|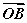 |·
|·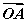 +|
+|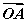 |·
|·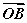 =0.将它类比到平面的情形是:若O是△ABC内一点,则有S△OBC·
=0.将它类比到平面的情形是:若O是△ABC内一点,则有S△OBC·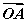 +S△OCA·
+S△OCA·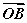 +S△OBA·
+S△OBA·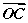 =
= ,将它类比到空间情形应该是:若O是四面体ABCD内一点,则有________.
,将它类比到空间情形应该是:若O是四面体ABCD内一点,则有________.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系中,以原点为极点, 轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度.已知曲线
轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度.已知曲线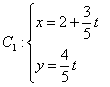 (
(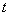 为参数)和曲线
为参数)和曲线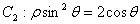 相交于
相交于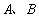 两点,设线段
两点,设线段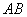 的中点为
的中点为 ,则点
,则点 的直角坐标为 .
的直角坐标为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
已知R为全集,A={x|(1-x)·(x+2)≤0},则∁RA=( )
A.{x|x<-2,或x>1} B.{x|x≤-2,或x≥1}
C.{x|-2<x<1} D.{x|-2≤x≤1}
查看答案和解析>>
科目:高中数学 来源: 题型:
设集合A={x|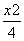 +
+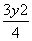 =1},B={y|y=x2},则A∩B=( )
=1},B={y|y=x2},则A∩B=( )
A.[-2,2] B.[0,2]
C.[0,+∞) D.{(-1,1),(1,1)}
查看答案和解析>>
科目:高中数学 来源: 题型:
设集合A={x|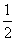 <2x<2},B={x|lgx>-1},则A∪B=( )
<2x<2},B={x|lgx>-1},则A∪B=( )
A.{x|x>-1} B.{x|-1<x<1}
C.{x|x>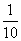 } D.{x|-1<x<10或x>10}
} D.{x|-1<x<10或x>10}
查看答案和解析>>
科目:高中数学 来源: 题型:
已知命题p:∃m∈R,m+1≤0,命题q:∀x∈R,x2+mx+1>0恒成立.若p∨q为假命题,则实数m的取值范围是( )
A.m≥2 B.m≤-2
C.m≤-2或m≥2 D.-2≤m≤2
查看答案和解析>>
科目:高中数学 来源: 题型:
方程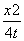 +
+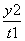 =1表示曲线C,给出以下命题:
=1表示曲线C,给出以下命题:
①曲线C不可能为圆;
②若1<t<4,则曲线C为椭圆;
③若曲线C为双曲线,则t<1或t>4;
④若曲线C为焦点在x轴上的椭圆,则1<t<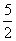 .
.
其中真命题的序号是______(写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
在给定的映射f:(x,y)→(2x+y,xy)(x,y∈R)作用下,点(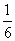 ,-
,-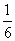 )的原像是( )
)的原像是( )
A.(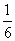 ,-
,-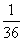 )
)
B.(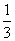 ,-
,-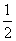 )或(-
)或(-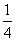 ,
, )
)
C.(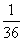 ,-
,-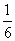 )
)
D.(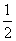 ,-
,-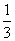 )或(-
)或(- ,
,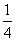 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com