
【题目】如图,在四棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 且
且![]() ,
, ![]() 分别为
分别为![]() 的中点.
的中点.
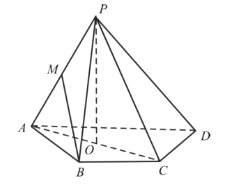
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)若二面角![]() 的大小为
的大小为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知线段AB的两个端点A、B分别在x轴和y轴上滑动,且∣AB∣=2.
(1)求线段AB的中点P的轨迹C的方程;
(2)求过点M(1,2)且和轨迹C相切的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 名学生分成
名学生分成![]() 两组参加城市绿化活动,其中
两组参加城市绿化活动,其中![]() 组布置
组布置![]() 盆盆景,
盆盆景, ![]() 组种植
组种植![]() 棵树苗.根据历年统计,每名学生每小时能够布置
棵树苗.根据历年统计,每名学生每小时能够布置![]() 盆盆景或者种植
盆盆景或者种植![]() 棵树苗.设布置盆景的学生有
棵树苗.设布置盆景的学生有![]() 人,布置完盆景所需要的时间为
人,布置完盆景所需要的时间为![]() ,其余学生种植树苗所需要的时间为
,其余学生种植树苗所需要的时间为![]() (单位:小时,可不为整数).
(单位:小时,可不为整数).
⑴写出![]() 、
、![]() 的解析式;
的解析式;
⑵比较![]() 、
、![]() 的大小,并写出这
的大小,并写出这![]() 名学生完成总任务的时间
名学生完成总任务的时间![]() 的解析式;
的解析式;
⑶应怎样分配学生,才能使得完成总任务的时间最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A的坐标为(4,1),点B(﹣7,﹣2)关于直线y=x的对称点为C.
(Ⅰ)求以A、C为直径的圆E的方程;
(Ⅱ)设经过点A的直线l与圆E的另一个交点为D,|AD|=8,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价为5元,销售单价与日均销售量的关系如图所示.
销售单价/元 | … | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | … |
日均销售量/桶 | … | 480 | 460 | 440 | 420 | 400 | 380 | … |
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设过抛物线y2=4x的焦点F的直线l交抛物线于点A,B,若以AB为直径的圆过点P(﹣1,2),且与x轴交于M(m,0),N(n,0)两点,则mn=( )
A.3
B.2
C.﹣3
D.﹣2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com