
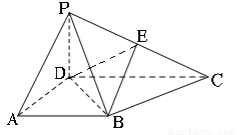
如图,在四棱锥P?ABCD中,PD⊥平面ABCD,AB∥CD,AD⊥CD,且AB=AD=PD=1,CD=2,E为PC的中点.
(1)求证:BE∥平面PAD;
(2)求二面角E?BD?C的余弦值.
(1)详见解析;(2)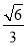 .
.
【解析】
试题分析:(1)要想证明线面平行,由线面平行的判定定理可知:只需证明此直线与平面内的某一直线平行即可,考虑到E为PC的中点,所以取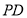 中点为
中点为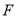 ,连接
,连接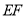 和AF;然后利用三角形的中位线的性质及空间中平行线的传递性可证BE//AF,再注意BE在平面PAD外,而AF在平面PAD内,从而可证BE∥平面PAD;(2)由已知可知直线DA、DC、DP两两互相垂直,所以我们可以
和AF;然后利用三角形的中位线的性质及空间中平行线的传递性可证BE//AF,再注意BE在平面PAD外,而AF在平面PAD内,从而可证BE∥平面PAD;(2)由已知可知直线DA、DC、DP两两互相垂直,所以我们可以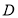 为原点,
为原点,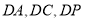 所在直线为
所在直线为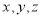 轴建立空间直角坐标系.从而由已知就可写出点P、C、A、B的坐标.进而因为E是PC的中点,求出E的坐标,然后就可写出平面BDE内不共线的两个向量的坐标,如
轴建立空间直角坐标系.从而由已知就可写出点P、C、A、B的坐标.进而因为E是PC的中点,求出E的坐标,然后就可写出平面BDE内不共线的两个向量的坐标,如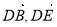 ,再设出平面BDE的一个法向量为
,再设出平面BDE的一个法向量为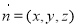 ,利用
,利用 可求出平面BDE的一个法向量;而平面BDC的一个法向量显然为:
可求出平面BDE的一个法向量;而平面BDC的一个法向量显然为: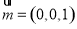 ,从而利用两法向量的夹角公式:
,从而利用两法向量的夹角公式: 就可求得所求二面角的余弦值.
就可求得所求二面角的余弦值.
试题解析:(1)证明:令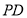 中点为
中点为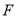 ,连接
,连接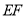 , 1分
, 1分
 点
点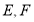 分别是
分别是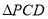 的中点,
的中点,

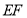
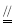
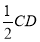 ,
,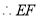
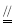
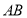 .
.
 四边形
四边形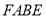 为平行四边形. 2分
为平行四边形. 2分
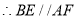 ,
,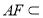 平面
平面 ,
,
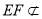 平面
平面 4分
4分
(三个条件少写一个不得该步骤分)
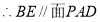 5分
5分
(2)以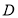 为原点,
为原点,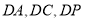 所在直线为
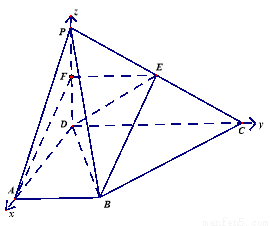
所在直线为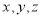 轴建立空间直角坐标系(如图).
轴建立空间直角坐标系(如图).
则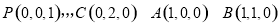 .
.
因为E是PC的中点,所以E的坐标为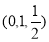 6分
6分
设平面DBE的一个法向量为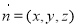 ,而
,而
则 令
令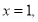 则
则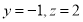 所以
所以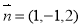 9分
9分
而平面DBC的一个法向量可为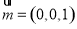
故 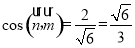 12分
12分
所以二面角E?BD?C的余弦值为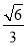 。 13分
。 13分
考点:1.线面平行;2.二面角.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源:2015届福建省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
某教室有4扇编号为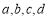 的窗户和2扇编号为
的窗户和2扇编号为 的门,窗户
的门,窗户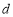 敞开,其余门和窗户均被关闭.为保持教室空气流通,班长在这些关闭的门和窗户中随机地敞开2扇.
敞开,其余门和窗户均被关闭.为保持教室空气流通,班长在这些关闭的门和窗户中随机地敞开2扇.
(Ⅰ)记“班长在这些关闭的门和窗户中随机地敞开2扇”为事件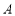 ,请列出事件
,请列出事件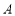 包含的基本事件;
包含的基本事件;
(Ⅱ)求至少有1扇门被班长敞开的概率.
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末文科数学试卷(解析版) 题型:解答题
设f(x)=ax3+bx+c为奇函数,其图象在点(1,f(1))处的切线与直线x-6y-7=0垂直,导函数f′(x)的最小值为-12.
(1)求a,b,c的值;
(2)求函数f(x)的单调递增区间,极大值和极小值,并求函数f(x)在[-1,3]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末文科数学试卷(解析版) 题型:选择题
设函数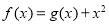 ,曲线
,曲线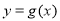 在点
在点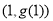 处的切线方程为
处的切线方程为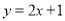 ,则曲线
,则曲线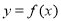 在点
在点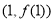 处切线的斜率为( )
处切线的斜率为( )
A.2 B.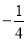 C.
C.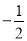 D.4
D.4
查看答案和解析>>
科目:高中数学 来源:2015届福建省等三校高二下学期期末理科数学试卷(解析版) 题型:解答题
如图,向量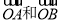 被矩阵M对应的变换
被矩阵M对应的变换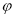 作用后分别变成
作用后分别变成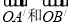 ,
,
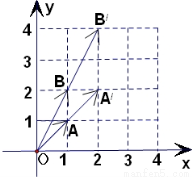
(1)求矩阵M;(2)求 在
在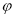 作用后的函数解析式.
作用后的函数解析式.
查看答案和解析>>
科目:高中数学 来源:2015届福建省等三校高二下学期期末理科数学试卷(解析版) 题型:填空题
设曲线C的参数方程为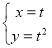 (t为参数),若以直角坐标系的原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为_______________.
(t为参数),若以直角坐标系的原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为_______________.
查看答案和解析>>
科目:高中数学 来源:2015届福建省四地六校高二下学期第一次月考理科数学试卷(解析版) 题型:选择题
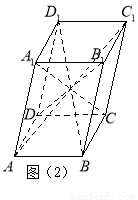
六个面都是平行四边形的四棱柱称为平行六面体。如,在平行四边形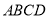 中,有
中,有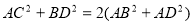 ,那么在图(2)的平行六面体
,那么在图(2)的平行六面体 中有
中有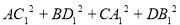 等于( )
等于( )

A.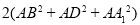 B.
B.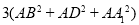
C.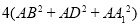 D.
D.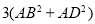
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com