
设f(x)=ax3+bx+c为奇函数,其图象在点(1,f(1))处的切线与直线x-6y-7=0垂直,导函数f′(x)的最小值为-12.
(1)求a,b,c的值;
(2)求函数f(x)的单调递增区间,极大值和极小值,并求函数f(x)在[-1,3]上的最大值与最小值.
(1)a=2,b=-12,c=0.;(2)函数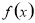 的单调递增区间为(-∞,-
的单调递增区间为(-∞,-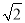 ),(
),(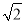 ,+∞).
,+∞).
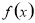 的极大值为
的极大值为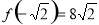 ,极小值为
,极小值为 又
又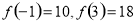 ,所以当
,所以当 时,
时,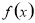 取得最小值为
取得最小值为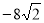 ,当x=3时
,当x=3时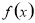 取得最大值1.
取得最大值1.
【解析】
试题分析:利用导数的几何意义求曲线在点(1,f(1))处的切线方程,注意这个点的切点.(2)解决类似的问题时,注意区分函数的最值和极值.求函数的最值时,要先求函数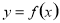 在区间
在区间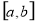 内使
内使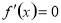 的点,再计算函数
的点,再计算函数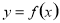 在区间内所有使
在区间内所有使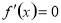 的点和区间端点处的函数值,最后比较即得.(3)分类讨论是学生在学习过程中的难点,要找好临界条件进行讨论.
的点和区间端点处的函数值,最后比较即得.(3)分类讨论是学生在学习过程中的难点,要找好临界条件进行讨论.
试题解析:(1)∵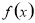 为奇函数,∴
为奇函数,∴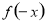
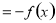 .
.
即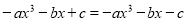 ∴
∴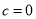 .∵
.∵ 的最小值为-12,∴
的最小值为-12,∴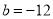 .
.
又直线x-6y-7=0的斜率为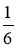 ,因此
,因此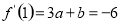 ,
,
故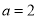 ,
,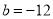 ,
,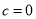 .
.
(2)f(x)=2x3-12x,f′(x)=6x2-12=6(x+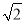 )(x-
)(x-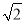 ),
),
列表如下
X | (-∞,- | - | (- |
| ( |
f′(x) | + | 0 | - | 0 | + |
f(x) |
| 极大 |
| 极小 |
|
所以函数f(x)的单调递增区间为(-∞,-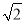 ),(
),(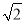 ,+∞).
,+∞).
f(x)的极大值为f(-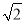 )=8
)=8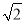 ,极小值为
,极小值为
f(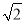 )=-8
)=-8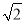
又f(-1)=10,f(3)=18,所以当x=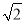 时,f(x)取得最小值为-8
时,f(x)取得最小值为-8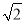 ,当x=3时f(x)取得最大值1
,当x=3时f(x)取得最大值1
考点:(1)由函数的性质求参量;(2)函数性质的应用 .


科目:高中数学 来源:2015届福建省高二上学期期中考试理科数学试卷(解析版) 题型:选择题
已知椭圆 的上、下顶点分别为
的上、下顶点分别为 、
、 ,左、右焦点分别为
,左、右焦点分别为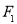 、
、 ,若四边形
,若四边形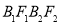 是正方形,则此椭圆的离心率
是正方形,则此椭圆的离心率 等于
等于
A. B.
B. C.
C. D.
D.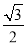
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末理科数学试卷(解析版) 题型:填空题
已知随机变量X服从正态分布N( 0,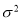 ),且P(-2≤X≤0)=0.4,则P(X>2)=________.
),且P(-2≤X≤0)=0.4,则P(X>2)=________.
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末理科数学试卷(解析版) 题型:选择题
某单位为了了解用电量y(度)与气温x(℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
气温x(℃) | 18 | 13 | 10 | -1 |
用电量y(度) | 24 | 34 | 38 | 64 |
由表中数据得线性回归方程 =
=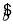 x+
x+ 中
中 ≈-2,预测当气温为-4℃时,用电量的度数约为( )
≈-2,预测当气温为-4℃时,用电量的度数约为( )
A.58 B.66 C.68 D.70
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末文科数学试卷(解析版) 题型:选择题
某公司租地建仓库,每月土地占用费y与仓库到车站的距离成反比,而每月库存货物费y与到车站的距离成正比,如果在距离车站10公里处建仓库,这这两项费用y和y分别为2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站
A.4公里处 B.5公里处 C.3公里处 D.2公里处
查看答案和解析>>
科目:高中数学 来源:2015届福建省等三校高二下学期期末理科数学试卷(解析版) 题型:解答题
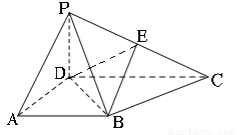
如图,在四棱锥P?ABCD中,PD⊥平面ABCD,AB∥CD,AD⊥CD,且AB=AD=PD=1,CD=2,E为PC的中点.
(1)求证:BE∥平面PAD;
(2)求二面角E?BD?C的余弦值.
查看答案和解析>>
科目:高中数学 来源:2015届福建省四地六校高二下学期第一次月考文科数学试卷(解析版) 题型:解答题
已知函数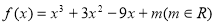 .
.
(1)求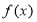 的极值(用含
的极值(用含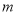 的式子表示);
的式子表示);
(2)若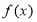 的图象与
的图象与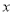 轴有3个不同交点,求
轴有3个不同交点,求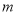 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com