【答案】
分析:(1)m=1时,求出焦点坐标以及a,b 的值,写出椭圆方程.
(2)由于△PF
1F
2周长为 2a+2c=6,故弦长|A
1A
2|=6,用点斜式设出直线L的方程,代入抛物线方程化简,得到根与系数的关系,代入弦长公式求出斜率 k的值.
解答:解:(1)当p=1时,F
2(1,0),F
1(-1,0)
设椭圆C
2的标准方程为
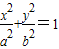
(a>b>0),∴c=1,
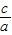
=

∵c
2=a
2-b
2,∴a=2,b=
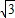
故椭圆C
2的标准方程为
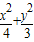
=1..(4分)
(2)(ⅰ)若直线l的斜率不存在,则l:x=1,且A(1,2),B(1,-2),∴|AB|=4
又∵△MF
1F
2的周长等于|MF
1|+|MF
2|+|F
1F
2|=2a+2c=6≠|AB|
∴直线l的斜率必存在.(6分)
(ⅱ)设直线l的斜率为k,则l:y=k(x-1)
由
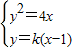
,得k
2x
2-(2k
2+4)x+k
2=0
∵直线l与抛物线C
1有两个交点A,B
∴△=[-(2k
2+4)]
2-4k
4=16k
2+16>0,且k≠0
设则可得
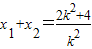
,x
1x
2=1
于是|AB|=
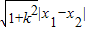
=
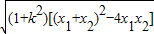
=
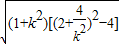
=
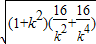
=
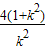
∵△MF
1F
2的周长等于|MF
1|+|MF
2|+|F
1F
2|=2a+2c=6
∴由
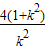
=6,解得k=
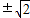
故所求直线l的方程为
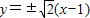
.(12分)
点评:本题考查抛物线和椭圆的标准方程和简单性质,弦长公式的应用,设出直线l的斜率为k,表示出△PF
1F
2的边长是解题的难点.

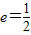 ;且抛物线C1和椭圆C2的一个交点记为M.
;且抛物线C1和椭圆C2的一个交点记为M.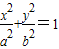 (a>b>0),∴c=1,
(a>b>0),∴c=1,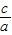 =
=
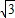
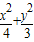 =1..(4分)
=1..(4分)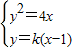 ,得k2x2-(2k2+4)x+k2=0
,得k2x2-(2k2+4)x+k2=0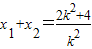 ,x1x2=1
,x1x2=1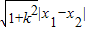 =
=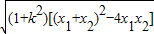
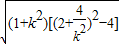
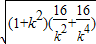 =
=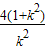
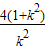 =6,解得k=
=6,解得k=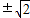
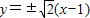 .(12分)
.(12分)

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 (2012•河北模拟)已知抛物线C1:y2=2px和圆C2:(x-
(2012•河北模拟)已知抛物线C1:y2=2px和圆C2:(x-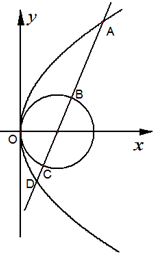 已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点F的直线l交C1于A,D两点(点A在x轴上方),直线l交C2于B,C两点(点B在x轴上方).
已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点F的直线l交C1于A,D两点(点A在x轴上方),直线l交C2于B,C两点(点B在x轴上方).