
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
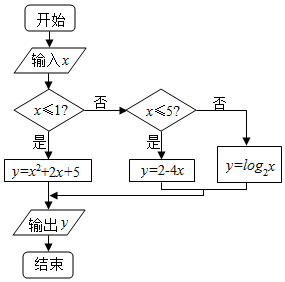
| A. | 2 | B. | ${log_2}\frac{π}{2}$ | C. | 2-2π | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
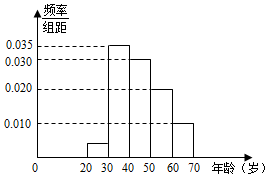 某市为庆祝北京夺得2022年冬奥会举办权,围绕“全民健身促健康,同心共筑中国梦”主题开展全民健身活动,组织方从参加活动的群众中随机抽取120名群众,按他们的年龄分组:第1组[20,30),第2组[30,40),第3组[40,50),第4组[50,60),第5组[60,70],得到的频率分布直方图如图所示.
某市为庆祝北京夺得2022年冬奥会举办权,围绕“全民健身促健康,同心共筑中国梦”主题开展全民健身活动,组织方从参加活动的群众中随机抽取120名群众,按他们的年龄分组:第1组[20,30),第2组[30,40),第3组[40,50),第4组[50,60),第5组[60,70],得到的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
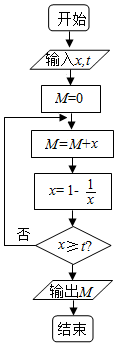
| A. | 3 | B. | $\frac{11}{3}$ | C. | $\frac{19}{6}$ | D. | $\frac{37}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
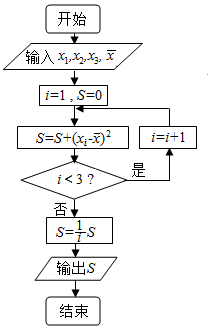
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com