
���� ��1������x=��cos�ȣ�y=��sin�����C1��C2��ֱ�����귽�̼��ɣ���2�����C3�IJ������̣����ݵ㵽ֱ�ߵľ��빫ʽ���㼴�ɣ�
��� �⣺��1����C1�ļ����귽���Ǧ�=$\frac{24}{4cos��+3sin��}$��
��4��cos��+3��sin��=11�������ã�4x+3y-24=0��
��C1��ֱ�����귽���ǣ�4x+3y-24=0��
����C2��$\left\{\begin{array}{l}{x=cos��}\\{y=sin��}\end{array}\right.$����x2+y2=1��
��C2����ͨ�����ǣ�x2+y2=1��
��2���ã�$\frac{x}{2\sqrt{2}}��\frac{y}{2}$����������C2����ͨ�����еģ�x��y����
�õ�����C3�ķ���Ϊ��$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1��
������C3�IJ��������ǣ�$\left\{\begin{array}{l}{x=2\sqrt{2}cos��}\\{y=2sin��}\end{array}\right.$��
��N��2$\sqrt{2}$cos����2sin���������N������C1�ľ����ǣ�
d=$\frac{|4��2\sqrt{2}cos��+3��2sin��-24|}{5}$
=$\frac{|2\sqrt{41}sin����+�ȣ�-24|}{5}$
=$\frac{24-2\sqrt{41}sin����+�ȣ�}{5}$��
��sin����+�ȣ�=1ʱ��d����Сֵ$\frac{24-2\sqrt{41}}{5}$��
��|MN|����Сֵ��$\frac{24-2\sqrt{41}}{5}$��
���� ���⿼���˼����귽���Լ��������̡���ͨ���̵�ת��������㵽ֱ�ߵľ��룬��һ���е��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\sqrt{3}$ | C�� | $\sqrt{2}$ | D�� | $\sqrt{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{x^2}{21}-\frac{y^2}{9}=1$ | B�� | $\frac{x^2}{9}-\frac{y^2}{21}=1$ | C�� | $\frac{x^2}{3}-\frac{y^2}{9}=1$ | D�� | $\frac{x^2}{9}-\frac{y^2}{3}=1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | ||
| C�� | ��һ��������� | D�� | �ڶ���������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
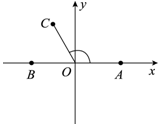 ����ͼ��ʾ��ƽ��ֱ������ϵ�У���֪��A��1��0���͵�B��-1��0����|$\overrightarrow{OC}$|=1���ҡ�AOC=x������OΪ����ԭ�㣮
����ͼ��ʾ��ƽ��ֱ������ϵ�У���֪��A��1��0���͵�B��-1��0����|$\overrightarrow{OC}$|=1���ҡ�AOC=x������OΪ����ԭ�㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com