
 如图所示在6×6的方格中,有A,B两个格子,则从该方格表中随机抽取一个矩形,该矩形包含格子A但不包含格子B的概率为$\frac{4}{21}$.
如图所示在6×6的方格中,有A,B两个格子,则从该方格表中随机抽取一个矩形,该矩形包含格子A但不包含格子B的概率为$\frac{4}{21}$. 分析 根据题意,假设水平方向的7条边依次为a1、a2、…a7,竖直方向的7条边依次为b1、b2、…b7;分析可得从该方格表中随机抽取一个矩形,需要在a1、a2、…a7中任选2条,在b1、b2、…b7中任选2条,即可组成一个矩形,由组合数公式计算可得可以抽取矩形的数目,进而分2种情况讨论矩形包含格子A但不包含格子B的取法,由古典概型计算公式计算即可得答案.
解答 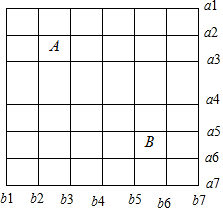 解:根据题意,如图假设水平方向的7条边依次为a1、a2、…a7,竖直方向的7条边依次为b1、b2、…b7,
解:根据题意,如图假设水平方向的7条边依次为a1、a2、…a7,竖直方向的7条边依次为b1、b2、…b7,
从该方格表中随机抽取一个矩形,需要在a1、a2、…a7中任选2条,在b1、b2、…b7中任选2条,即可组成一个矩形,
则一共可以抽取C72×C72=21×21=441个矩形;
该矩形包含格子A但不包含格子B,
分2种情况讨论:
①、在a1、a2中任选1条,a3、a4、a5中任选1条,在b1、b2中任选1条,b3、b4、…b7中任选1条,有C21C31×C21C51种取法,
②、在b1、b2中任选1条,b3、b4、b5中任选1条,在a1、a2中任选1条,a3、a4、…a7中任选1条,有C21C31×C21C51种取法,
其中重复的有C21C31×C21C31种取法,
则矩形包含格子A但不包含格子B的取法有2(C21C31×C21C51)-C21C31×C21C31=84种,
故该矩形包含格子A但不包含格子B的概率P=$\frac{84}{441}$=$\frac{4}{21}$;
故答案为:$\frac{4}{21}$.
点评 本题考查古典概率的计算,涉及排列、组合的应用,关键是由排列、组合公式计算得到随机抽取一个矩形的数目.


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:解答题
 已知某企业近3年的前7好个月的月利润(单位:百万元)如下的折线图所示:
已知某企业近3年的前7好个月的月利润(单位:百万元)如下的折线图所示:| 月份x | 1 | 2 | 3 | 4 |
| 利润y(单位:百万元) | 4 | 4 | 6 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=1时,y极大值=0 | B. | x=e时,y极大值=$\frac{1}{e^2}$ | ||
| C. | x=e时,y极小值=$\frac{1}{e^2}$ | D. | $x=\sqrt{e}$时,y极大值=$\frac{1}{2e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com