
【题目】已知![]() 的内角A,B,C的对边分别为a,b,c,且满足
的内角A,B,C的对边分别为a,b,c,且满足![]() .
.
(1)求角![]() ;
;
(2)若![]() ,___________________(从下列问题中任选一个作答,若选择多个条件分别解答,则按选择的第一个解答计分).
,___________________(从下列问题中任选一个作答,若选择多个条件分别解答,则按选择的第一个解答计分).
①![]() 的面积为
的面积为![]() ,求
,求![]() 的周长;
的周长;
②![]() 的周长为21,求
的周长为21,求![]() 的面积.
的面积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】“辛卜生公式”给出了求几何体体积的一种计算方法:夹在两个平行平面之间的几何体,如果被平行于这两个平面的任何平面所截,截得的截面面积是截面高的(不超过三次)多项式函数,那么这个几何体的体积,就等于其上底面积、下底面积与四倍中截面面积的和乘以高的六分之一.即![]() ,式中
,式中![]() ,
,![]() ,
,![]() ,
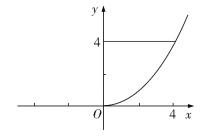
,![]() 依次为几何体的高、上底面积、下底面积、中截面面积.如图,现将曲线
依次为几何体的高、上底面积、下底面积、中截面面积.如图,现将曲线![]() 与直线
与直线![]() 及
及![]() 轴围成的封闭图形绕
轴围成的封闭图形绕![]() 轴旋转一周得到一个几何体,则利用辛卜生公式可求得该几何体的体积为( )
轴旋转一周得到一个几何体,则利用辛卜生公式可求得该几何体的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.16
D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
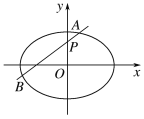
【题目】如图,椭圆E:![]() +
+![]() =1(a>b>0)的离心率是
=1(a>b>0)的离心率是![]() ,过点P(0,1)的动直线l与椭圆相交于A,B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为2
,过点P(0,1)的动直线l与椭圆相交于A,B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为2![]() .
.
(1)求椭圆E的方程;
(2)在平面直角坐标系xOy中,是否存在与点P不同的定点Q,使得![]() =
=![]() 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ax3+bx2+cx(a≠0)在x=±1时取得极值,且f(1)=-1.
(1)试求常数a、b、c的值;
(2)试判断x=±1是函数的极小值还是极大值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机运动计步已经成为一种新时尚.某单位统计了职工一天行走步数(单位:百步),绘制出如下频率分布直方图:
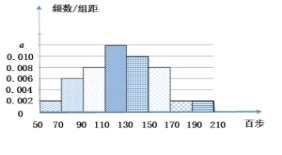
(1)求直方图中a的值,并由频率分布直方图估计该单位职工一天步行数的中位数;
(2)若该单位有职工200人,试估计职工一天行走步数不大于13000的人数;
(3)在(2)的条件下,该单位从行走步数大于15000的3组职工中用分层抽样的方法选取6人参加远足拉练活动,再从6人中选取2人担任领队,求这两人均来自区间![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com