【题目】已知数列
满足
， 
．
（1）证明数列
是等比数列；
（2）求数列
的前
项和
．
【答案】(1)见解析(2) 
【解析】试题分析：（1）要证明数列
是等比数列，即证明
（常数），根据
代入即可证明；（2）根据（1）的结果，可知
，
，当
时，
，所以求
的和时，可先分
时，
，当时，
，最后验证是否成立.
试题解析：（1）∵
，∴
．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．1分
∵
，∴
．．．．．．．．．．．．．3分
∴
．．．．．．．．．．．．．．．．．．．．．．．．．．．．4分
∴
是以2为首项，2为公比的等比数列．．．．．．．．．．．．．．．．．．．．．．．．．．．．5分
（2）由（1），可知
，∴
．．．．．．．．．．．．．．．．．．．．．7分
当
时， 
，∴
；．．．．．．．．．．．．．．．．．．．．．．．．．．．8分
当
时， 
，
∴
．．．．．．．．．．．．．．．．．．．．9分
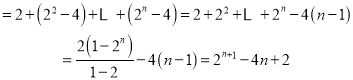
……………………………11分
又当
时，上式也满足．
∴当
时， 
．．．．．．．．．．．．．．．．．．．．12分
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=Acos（ 
+ 
），x∈R，且f（ 
）= 
．
（1）求A的值；
（2）设α，β∈[0， 
]，f（4α+ 
π）=﹣ 
，f（4β﹣ 
π）= 
，求cos（α+β）的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
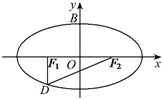
【题目】如图，设椭圆
（
）的左、右焦点分别为
，点
在椭圆上， 
， 
， 
的面积为
.
（Ⅰ）求该椭圆的标准方程；
（Ⅱ）是否存在圆心在
轴上的圆，使圆在
轴的上方与椭圆
有两个交点，且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点？若存在，求圆的方程，若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】现有0，1，2，3，4，5六个数字．
（1）用所给数字能够组成多少个四位数？
（2）用所给数字可以组成多少个没有重复数字的五位数？
（3）用所给数字可以组成多少个没有重复数字且比3142大的数？（最后结果均用数字作答）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
