
【题目】已知p:|1﹣ ![]() |≤2,q:x2﹣2x+1﹣m2≤0(m>0).若“非p”是“非q”的必要而不充分条件,求实数m的取值范围.
|≤2,q:x2﹣2x+1﹣m2≤0(m>0).若“非p”是“非q”的必要而不充分条件,求实数m的取值范围.
【答案】解:解法一:由p:|1﹣ ![]() |≤2,解得﹣2≤x≤10, ∴“非p”:A={x|x>10或x<﹣2}、(3分)
|≤2,解得﹣2≤x≤10, ∴“非p”:A={x|x>10或x<﹣2}、(3分)
由q:x2﹣2x+1﹣m2≤0,解得1﹣m≤x≤1+m(m>0)
∴“非q”:B={x|x>1+m或x<1﹣m,m>0=(6分)
由“非p”是“非q”的必要而不充分条件可知:BA. 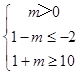 解得m≥9.
解得m≥9.
∴满足条件的m的取值范围为{m|m≥9}.(12分)
解法二:由“非p”是“非q”的必要而不充分条件.即“非q”“非p”,但“非p” ![]() “非q”,可以等价转换为它的逆否命题:“pq,但q
“非q”,可以等价转换为它的逆否命题:“pq,但q ![]() p”.即p是q的充分而不必要条件.
p”.即p是q的充分而不必要条件.
由|1﹣ ![]() |≤2,解得﹣2≤x≤10,
|≤2,解得﹣2≤x≤10,
∴p={x|﹣2≤x≤10}
由x2﹣2x+1﹣m2≤0,解得1﹣m≤x≤1+m(m>0)
∴q={x|1﹣m≤x≤1+m,m>0}
由p是q的充分而不必要条件可知:
pq 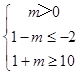 解得m≥9.
解得m≥9.
∴满足条件的m的取值范围为{m|m≥9}
【解析】思路一:“按题索骥”﹣﹣解不等式,求否命题,再根据充要条件的集合表示进行求解;思路二:本题也可以根据四种命题间的关系进行等价转换,然后再根据充要条件的集合表示进行求解.
【考点精析】本题主要考查了解一元二次不等式和绝对值不等式的解法的相关知识点,需要掌握求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边;含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能正确解答此题.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边;含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】对定义域分别为D1 , D2的函数y=f(x),y=g(x),规定:函数h(x)= 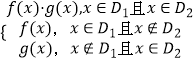 ,f(x)=x﹣2(x≥1),g(x)=﹣2x+3(x≤2),则h(x)的单调减区间是 .
,f(x)=x﹣2(x≥1),g(x)=﹣2x+3(x≤2),则h(x)的单调减区间是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,抛物线y=1﹣x2与x轴所围成的区域是一块等待开垦的土地,现计划在该区域内围出一块矩形地块ABCD作为工业用地,其中A、B在抛物线上,C、D在x轴上.已知工业用地每单位面积价值为3a元(a>0),其它的三个边角地块每单位面积价值a元.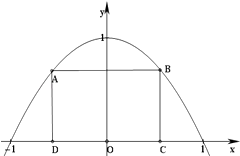
(1)求等待开垦土地的面积;
(2)如何确定点C的位置,才能使得整块土地总价值最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足 ![]() ,
, ![]() .
.
(1)求函数f(x)的解析式;
(2)求函数g(x)的单调区间;
(3)如果s、t、r满足|s﹣r|≤|t﹣r|,那么称s比t更靠近r.当a≥2且x≥1时,试比较 ![]() 和ex﹣1+a哪个更靠近lnx,并说明理由.
和ex﹣1+a哪个更靠近lnx,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com