
分析 (1)通过连结FQ,利用中垂线的性质及椭圆的定义即得结论;
(2)证明:设P(x0,y0),可得3x02=4(3-y02),直线B1P的方程为:y=$\frac{{y}_{0}+\sqrt{3}}{{x}_{0}}x-\sqrt{3}$.令y=0,得${x}_{C}=\frac{\sqrt{3}{x}_{0}}{\sqrt{3}+{y}_{0}},同理得{x}_{D}=\frac{\sqrt{3}{x}_{0}}{\sqrt{3}-{y}_{0}}$,
|OC|•|OD|=|xC|•|xD|=|$\frac{3{{x}_{0}}^{2}}{3-{{y}_{0}}^{2}}$|=4(定值);
(3)当点C的坐标为(-1,0)时,点D(-4,0),|CD|=3,
设直线l的方程为:x=my-1,A(x1,y1),B(x2,y2)
联立$\left\{\begin{array}{l}{x=my-1}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$得(3m2+4)y2-6my-9=0
解得:${y}_{1}=\frac{3m-6\sqrt{{m}^{2}+1}}{3{m}^{2}+4},{y}_{2}=\frac{3m+\sqrt{{m}^{2}+1}}{3{m}^{2}+4}$.
|y1-y2|=$\frac{12\sqrt{{m}^{2}+1}}{3{m}^{2}+4}$,△ABD面积s=$\frac{1}{2}$×|y1-y2|=$\frac{3}{2}$$\frac{12\sqrt{{m}^{2}+1}}{3{m}^{2}+4}$=$\frac{18\sqrt{{m}^{2}+1}}{3{m}^{2}+4}$=$\frac{18}{3\sqrt{{m}^{2}+1}+\frac{1}{\sqrt{{m}^{2}+1}}}$;
解答 (1)解:连结FQ,则FQ=NQ,
∵MQ+FQ=MQ+QN=MN=4>ME,椭圆的定义即得点Q的轨迹为以点M、F为焦点,长轴为4的椭圆
∴2a=4,即a=2,又∵焦点为(1,0),即c=1,
∴b2=a2-c2=4-1=3,
故点Q的轨迹C的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$
(2)证明:设P(x0,y0),直线B1P的方程为:y=$\frac{{y}_{0}+\sqrt{3}}{{x}_{0}}x-\sqrt{3}$.
令y=0,得${x}_{C}=\frac{\sqrt{3}{x}_{0}}{\sqrt{3}+{y}_{0}},同理得{x}_{D}=\frac{\sqrt{3}{x}_{0}}{\sqrt{3}-{y}_{0}}$,
|OC|•|OD|=|xC|•|xD|=|$\frac{3{{x}_{0}}^{2}}{3-{{y}_{0}}^{2}}$|
∵点P是曲线E上但不在坐标轴上的任意一点,∴$\frac{{{x}_{0}}^{2}}{4}+\frac{{{y}_{0}}^{2}}{3}=1$.即3x02=4(3-y02),
∴$\frac{{{x}_{0}}^{2}}{4}+\frac{{{y}_{0}}^{2}}{3}=1$=4,|OC|•|OD|是否为定值4.
(3)当点C的坐标为(-1,0)时,点D(-4,0),|CD|=3,
设直线l的方程为:x=my-1,A(x1,y1),B(x2,y2)
联立$\left\{\begin{array}{l}{x=my-1}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$得(3m2+4)y2-6my-9=0
解得:${y}_{1}=\frac{3m-6\sqrt{{m}^{2}+1}}{3{m}^{2}+4},{y}_{2}=\frac{3m+\sqrt{{m}^{2}+1}}{3{m}^{2}+4}$.
|y1-y2|=$\frac{12\sqrt{{m}^{2}+1}}{3{m}^{2}+4}$,△ABD面积s=$\frac{1}{2}$×|y1-y2|=$\frac{3}{2}$•$\frac{12\sqrt{{m}^{2}+1}}{3{m}^{2}+4}$=$\frac{18\sqrt{{m}^{2}+1}}{3{m}^{2}+4}$=$\frac{18}{3\sqrt{{m}^{2}+1}+\frac{1}{\sqrt{{m}^{2}+1}}}$;
∵$\sqrt{{m}^{2}+1}≥1$,根据∵$y=3x+\frac{1}{x}$在[1,+∞)递增 可得3$\sqrt{{m}^{2}+1}+\frac{1}{\sqrt{{m}^{2}+1}}≥4$.
∴$s≤\frac{18}{4}=\frac{9}{2}$
∴m=0,即直线AB:x=-1时,△ABD面积的最大为$\frac{9}{2}$.
点评 本题考查了轨迹方程的求法,直线与椭圆的位置关系,主要考查运算能力,属于难题.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,E为PB上任意一点.
如图,已知四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,E为PB上任意一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
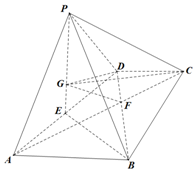 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为梯形,AB∥CD,AB=2DC=2$\sqrt{3}$,AC∩BD=F.且△PAD与△ABD均为正三角形,E为AD的中点,G为△PAD重心.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为梯形,AB∥CD,AB=2DC=2$\sqrt{3}$,AC∩BD=F.且△PAD与△ABD均为正三角形,E为AD的中点,G为△PAD重心.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M=N | B. | M∩N=N | C. | M∪N=N | D. | M∩N=∅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com