
| A. | 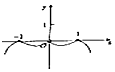 | B. |  | C. |  | D. |  |
分析 利用函数的奇偶性排除选项,特殊值的位置判断求解即可.
解答 解:函数$y=\frac{{{x^2}ln{x^2}}}{|x|}$是偶函数,排除B,x=e时,y=e,即(e,e)在函数的图象上,排除A,
当x=$\frac{1}{e}$时,y=$-\frac{2}{e}$,当x=$\frac{1}{{e}^{2}}$时,y=-$\frac{\frac{1}{{e}^{4}}ln{e}^{-4}}{\frac{1}{{e}^{2}}}$=$-\frac{4}{{e}^{2}}$,$-\frac{2}{e}<-\frac{4}{{e}^{2}}$,
可知($\frac{1}{e}$,$-\frac{2}{e}$)在($\frac{1}{{e}^{2}},-\frac{4}{{e}^{4}}$)的下方,
排除C.
故选:D.
点评 本题考查函数的图象的判断与应用,考查转化思想以及计算能力.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:解答题
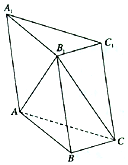 如图所示,已知三棱柱ABC-A1B1C1中,A1C1=B1C1,A1A=A1B1,∠AA1B1=60°.
如图所示,已知三棱柱ABC-A1B1C1中,A1C1=B1C1,A1A=A1B1,∠AA1B1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 8π | C. | 16π | D. | 20π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
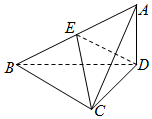 已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.
已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
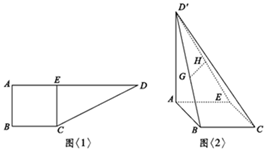 如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D′EC的位置,使D′A=2$\sqrt{3}$,如图<2>:若G,H分别为D′B,D′E的中点.
如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D′EC的位置,使D′A=2$\sqrt{3}$,如图<2>:若G,H分别为D′B,D′E的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com