
分析 (1)求出函数y=$\frac{{x}^{2}}{2p}$的导数,可得切线的斜率,由两直线垂直的条件:斜率之积为-1,再将直线y=x+1代入抛物线方程,运用韦达定理,解方程可得p的值,进而得到抛物线的方程;
(2)将直线y=k(x-1)+2代入抛物线方程x2=4y,运用韦达定理和弦长公式,求得|AB|,再由切线的方程求出交点H的坐标,运用点到直线的距离公式,结合三角形的面积公式可得S1,再由直线AB与抛物线G围成封闭图形的面积为S2=${∫}_{{x}_{1}}^{{x}_{2}}$[k(x-1)+2-$\frac{1}{4}$x2]dx,化简计算即可得到面积的比值为定值.
解答 解:(1)x2=2py(p>0),即y=$\frac{{x}^{2}}{2p}$,
导数为y′=$\frac{x}{p}$,切线L1,L2的斜率分别为$\frac{{x}_{1}}{p}$,$\frac{{x}_{2}}{p}$,
L1⊥L2,可得$\frac{{x}_{1}}{p}$•$\frac{{x}_{2}}{p}$=-1,
联立直线y=x+1和x2=2py(p>0),
可得x2-2px-2p=0,即有x1x2=-2p,
即有-p2=-2p,解得p=2,
则抛物线G的方程为x2=4y;
(2)证明:将直线y=k(x-1)+2代入抛物线方程x2=4y,
可得x2-4kx+4k-8=0,
即有x1+x2=4k,x1x2=4k-8,
x1<x2,可得x2-x1=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{16{k}^{2}-16k+32}$=4$\sqrt{{k}^{2}-k+2}$.
抛物线的方程为y=$\frac{1}{4}$x2,求导得y′=$\frac{1}{2}$x,
过抛物线上A、B两点的切线方程分别是y-y1=$\frac{1}{2}$x1(x-x1),y-y2=$\frac{1}{2}$x2(x-x2),
即y=$\frac{1}{2}$x1x-$\frac{1}{4}$x12,y=$\frac{1}{2}$x2x-$\frac{1}{4}$x22,
解得两条切线l1、l2的交点H的坐标为($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{x}_{1}{x}_{2}}{4}$),即H(2k,k-2).
可得H到直线y=k(x-1)+2的距离为d=$\frac{|k(2k-1)+2-k+2|}{\sqrt{1+{k}^{2}}}$=$\frac{2({k}^{2}-k+2)}{\sqrt{1+{k}^{2}}}$,
|AB|=$\sqrt{1+{k}^{2}}$•|x2-x1|=4$\sqrt{1+{k}^{2}}$•$\sqrt{{k}^{2}-k+2}$.
可得△ABH的面积为S1=$\frac{1}{2}$d•|AB|=$\frac{1}{2}$•$\frac{2({k}^{2}-k+2)}{\sqrt{1+{k}^{2}}}$•4$\sqrt{1+{k}^{2}}$•$\sqrt{{k}^{2}-k+2}$
=4(k2-k+2)•$\sqrt{{k}^{2}-k+2}$.
直线AB与抛物线G围成封闭图形的面积为S2=${∫}_{{x}_{1}}^{{x}_{2}}$[k(x-1)+2-$\frac{1}{4}$x2]dx
=[$\frac{1}{2}$kx2+(2-k)x-$\frac{1}{12}$x3]|${\;}_{{x}_{1}}^{{x}_{2}}$=$\frac{1}{2}$k(x2-x1)(x2+x1)+(2-k)(x2-x1)-$\frac{1}{12}$(x2-x1)[(x2+x1)2-x1x2]
=(x2-x1)[2k2+2-k-$\frac{1}{12}$(16k2-4k+8)]=4$\sqrt{{k}^{2}-k+2}$•$\frac{2}{3}$(k2-k+2)=$\frac{8}{3}$(k2-k+2)•$\sqrt{{k}^{2}-k+2}$.
则$\frac{S_1}{S_2}$为定值$\frac{3}{2}$.
点评 本题考查直线和抛物线的位置关系,注意运用联立方程,运用韦达定理,以及弦长公式和点到直线的距离公式,考查运用定积分求不规则图形的面积,考查化简整理的运算能力,是一道综合题.


科目:高中数学 来源: 题型:解答题
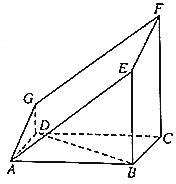 如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.
如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
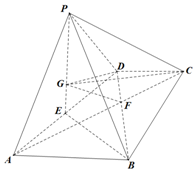 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为梯形,AB∥CD,AB=2DC=2$\sqrt{3}$,AC∩BD=F.且△PAD与△ABD均为正三角形,E为AD的中点,G为△PAD重心.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为梯形,AB∥CD,AB=2DC=2$\sqrt{3}$,AC∩BD=F.且△PAD与△ABD均为正三角形,E为AD的中点,G为△PAD重心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知如图:三棱柱ABC-A1B1C1的各条棱均相等,AA1⊥平面ABC,E为AA1的中点.
已知如图:三棱柱ABC-A1B1C1的各条棱均相等,AA1⊥平面ABC,E为AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com