
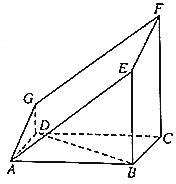
 如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.
如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.分析 (Ⅰ)由余弦定理得BD=$\sqrt{3}$,满足AB2=AD2+DB2,得AD⊥DB,直平行六面体中GD⊥面ABCD,得BD⊥平面ADG.
(Ⅱ)如图以D为原点建立空间直角坐标系D-xyz,求出法向量,利用公式求解.
解答 解:(Ⅰ)证明:在△BAD中,∵AB=2AD=2,∠BAD=60°.
由余弦定理得BD=$\sqrt{3}$,满足AB2=AD2+DB2,∴AD⊥DB
直平行六面体中GD⊥面ABCD,DB?面ABCD,∴GD⊥DB,且AD∩GD=D
∴BD⊥平面ADG.
(Ⅱ)如图以D为原点建立空间直角坐标系D-xyz,
∵∠BAE=∠GAD=45°,AB=2AD=2,∴A(1,0,0),B(0,$\sqrt{3}$,0),E(0,$\sqrt{3}$,2),C(-1,$\sqrt{3,}0)$.
$\overrightarrow{AE}=(-1,\sqrt{3},2),\overrightarrow{AG}=(-1,0,1)$,
设平面AEFG的法向量$\overrightarrow{n}=(x,y,z)$,
$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AE}=-x+\sqrt{3}y+2z=0}\\{\overrightarrow{n}•\overrightarrow{AG}=-x+z=0}\end{array}\right.$,令x=1,得y=$-\frac{\sqrt{3}}{3}$,z=1
∴$\overrightarrow{n}=(1,-\frac{\sqrt{3}}{3},1)$,而平面ABCD的法向量为$\overrightarrow{DG}=(0,0,1)$
∴$cos<\overrightarrow{DG},\overrightarrow{n}>=\frac{\overrightarrow{DG}•\overrightarrow{n}}{|\\;\overrightarrow{DG}|\\;|\\;\overrightarrow{n}|\\;}=\frac{\sqrt{21}}{7}$.
∴平面AEFG与平面ABCD所成锐二面角的余弦值为$\frac{\sqrt{21}}{7}$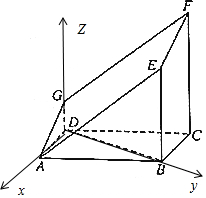
点评 本题考查了空间线面垂直的判定,及向量法求二面角,属于中档题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | {4} | B. | {1} | C. | {4,5} | D. | {1,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
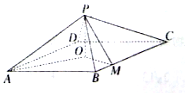 如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面$ABCD,AB=2,∠BAD=\frac{π}{3},M$为BC上一点,且$BM=\frac{1}{2}$.
如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面$ABCD,AB=2,∠BAD=\frac{π}{3},M$为BC上一点,且$BM=\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3-2\sqrt{2}}{8}$ | B. | $\frac{2-\sqrt{2}}{4}$ | C. | $\frac{5-2\sqrt{2}}{8}$ | D. | $\frac{5-2\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
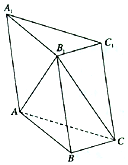 如图所示,已知三棱柱ABC-A1B1C1中,A1C1=B1C1,A1A=A1B1,∠AA1B1=60°.
如图所示,已知三棱柱ABC-A1B1C1中,A1C1=B1C1,A1A=A1B1,∠AA1B1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某校高三文科班150名男生在“学生体质健康50米跑”单项测试中,成绩全部介于6秒与11秒之间.现将测试结果分成五组:第一组[6,7];第二组(7,8],…,第五组(10,11].如图是按上述分组方法得到的频率分布直方图.按国家标准,高三男生50米跑成绩小于或等于7秒认定为优秀,若已知第四组共48人,则该校文科班男生在这次测试中成绩优秀的人数是9.
某校高三文科班150名男生在“学生体质健康50米跑”单项测试中,成绩全部介于6秒与11秒之间.现将测试结果分成五组:第一组[6,7];第二组(7,8],…,第五组(10,11].如图是按上述分组方法得到的频率分布直方图.按国家标准,高三男生50米跑成绩小于或等于7秒认定为优秀,若已知第四组共48人,则该校文科班男生在这次测试中成绩优秀的人数是9.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com