
 如图,已知四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,E为PB上任意一点.
如图,已知四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,E为PB上任意一点.分析 (1)连结AC,BD,推导出AC⊥BD,AC⊥PD,从而AC⊥平面PBD,由此能证明平面EAC⊥平面PBD.
(2)由$\frac{{V}_{E-ABC}}{{V}_{P-ABCD}}$=$\frac{1}{4}$,能求出E为PB的中点.
解答 证明:(1)连结AC,BD,
∵底面ABCD是菱形,∴AC⊥BD,
∵PD⊥平面ABCD,AC?平面ABCD,
∴AC⊥PD,
∵BD∩PD=D,∴AC⊥平面PBD,
∵AC?平面EAC,∴平面EAC⊥平面PBD.
解:(2)∵四棱锥P-ABCD的体积等于三棱锥B-ACE体积的4倍,
∴$\frac{{V}_{E-ABC}}{{V}_{P-ABCD}}$=$\frac{1}{4}$,
设P到平面ABCD的距离为h,
则$\frac{{V}_{E-ABC}}{{V}_{P-ABCD}}$=$\frac{\frac{1}{3}×{S}_{△ABC}×h}{\frac{1}{3}×2{S}_{△ABC}×PD}$=$\frac{h}{2PD}$=$\frac{1}{4}$,
解得h=$\frac{1}{2}$PD,
故此时E为PB的中点.
点评 本题考查面面垂直的证明,考查满足条件的点的位置的确定,是中档题,解题时要认真审题,注意空间思维能力的培养.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
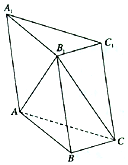 如图所示,已知三棱柱ABC-A1B1C1中,A1C1=B1C1,A1A=A1B1,∠AA1B1=60°.
如图所示,已知三棱柱ABC-A1B1C1中,A1C1=B1C1,A1A=A1B1,∠AA1B1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某校高三文科班150名男生在“学生体质健康50米跑”单项测试中,成绩全部介于6秒与11秒之间.现将测试结果分成五组:第一组[6,7];第二组(7,8],…,第五组(10,11].如图是按上述分组方法得到的频率分布直方图.按国家标准,高三男生50米跑成绩小于或等于7秒认定为优秀,若已知第四组共48人,则该校文科班男生在这次测试中成绩优秀的人数是9.
某校高三文科班150名男生在“学生体质健康50米跑”单项测试中,成绩全部介于6秒与11秒之间.现将测试结果分成五组:第一组[6,7];第二组(7,8],…,第五组(10,11].如图是按上述分组方法得到的频率分布直方图.按国家标准,高三男生50米跑成绩小于或等于7秒认定为优秀,若已知第四组共48人,则该校文科班男生在这次测试中成绩优秀的人数是9.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 55% | B. | 65% | C. | 75% | D. | 80% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
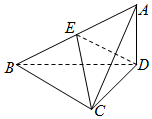 已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.
已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com