
���� ���������ø����ǹ�ʽ�����Һ�����ͼ������ʣ��ó����ۣ�
��� �⣺�ߺ���$f��x��=cos2x+\sqrt{3}sin2x$=2��$\frac{1}{2}$cos2x+$\frac{\sqrt{3}}{2}$sin2x��=2cos��2x-$\frac{��}{3}$����
�ʢ���ȷ��
�ߵ�$x=k��+\frac{��}{6}$��k��Z��ʱ������f��x��ȡ�����ֵΪ2���ʢ���ȷ��
��x1��x2����f��x1��=f��x2��=0����x1��x2Ϊ����f��x������㣬x1��x2��������ڵ���������
��${x_1}-{x_2}=\frac{k��}{2}��k��Z��k��0��$���ʢ���ȷ��
��x=$\frac{2��}{3}$ʱ��f��x��=2cos��=-2��Ϊ��������Сֵ���ʺ���f��x����ͼ�����ֱ��$x=\frac{2��}{3}$�Գƣ�
�ʢ���ȷ��
�ʴ�Ϊ���٢ڢۢܣ�
���� ������Ҫ���鸨���ǹ�ʽ�����Һ�����ͼ������ʣ������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{4}{5}$ | B�� | $\frac{3}{5}$ | C�� | $-\frac{3}{5}$ | D�� | $-\frac{4}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
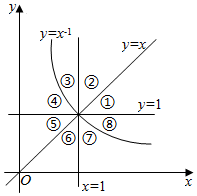 ��ͼ������$y=\frac{1}{x}$��y=x��y=1��ͼ���ֱ��x=1��ƽ��ֱ������ϵ�ĵ�һ���ֳɰ˸����֣��٢ڢۢܢݢޢߢ࣮���ݺ���f��x����ͼ���IJ����Ǣܢ࣬��f��x�������ǣ�������
��ͼ������$y=\frac{1}{x}$��y=x��y=1��ͼ���ֱ��x=1��ƽ��ֱ������ϵ�ĵ�һ���ֳɰ˸����֣��٢ڢۢܢݢޢߢ࣮���ݺ���f��x����ͼ���IJ����Ǣܢ࣬��f��x�������ǣ�������| A�� | y=x2 | B�� | $y=\frac{1}{{\sqrt{x}}}$ | C�� | $y={x^{\frac{1}{2}}}$ | D�� | y=x-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com