练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．为评估一种农作物的种植效果，选了n块地作试验田．这n块地的亩产量（单位：kg）分别是x1，x2，…，xn，下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是（　　）
    A．x1，x2，…，xn的平均数B．x1，x2，…，xn的标准差
    C．x1，x2，…，xn的最大值D．x1，x2，…，xn的中位数

    分析 利用平均数、标准差、最大值、中位数的定义和意义直接求解．

    解答 解：在A中，平均数是表示一组数据集中趋势的量数，它是反映数据集中趋势的一项指标，
    故A不可以用来评估这种农作物亩产量稳定程度；
    在B 中，标准差能反映一个数据集的离散程度，故B可以用来评估这种农作物亩产量稳定程度；
    在C中，最大值是一组数据最大的量，故C不可以用来评估这种农作物亩产量稳定程度；
    在D中，中位数将数据分成前半部分和后半部分，用来代表一组数据的“中等水平”，
    故D不可以用来评估这种农作物亩产量稳定程度．
    故选：B．

    点评 本题考查可以用来评估这种农作物亩产量稳定程度的量的判断，是基础题，解题时要认真审题，注意平均数、标准差、最大值、中位数的定义和意义的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．如图，已知正方形ABCD和矩形ACEF所在平面相互垂直，$AB=\sqrt{2}，AF=1$，M在线段EF上．
    （1）若M是线段EF的中点，证明：平面AMD⊥平面BDF；
    （2）命题“若M为线段EF的中点，则平面ADM⊥平面BDF”的逆命题是否成立？若成立，给出证明，否则请举出反例．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．如图，平行四边形PABC中，∠PAC=∠ABC=90°，PA=AB=2$\sqrt{3}$，AC=4，现把△PAC沿AC折起，使PA与平面ABC成60°角，设此时P在平面ABC上的投影为O点（O与B在AC的同侧）．

    （Ⅰ）求证：OB∥平面PAC；
    （Ⅱ）试问：线段PA上是否在存在一点M，使得二面角M-BC-A的余弦值为$\frac{5\sqrt{37}}{37}$？若存在，指出M的位置，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

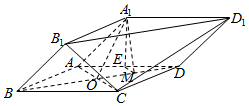    2．由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示，四边形ABCD为正方形，O为AC与BD 的交点，E为AD的中点，A1E⊥平面ABCD，
    （Ⅰ）证明：A1O∥平面B1CD1；
    （Ⅱ）设M是OD的中点，证明：平面A1EM⊥平面B1CD1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知a、b∈R，（a+bi）2=3+4i（i是虚数单位），则a2+b2=5，ab=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知向量$\overrightarrow{a}$=（-1，2），$\overrightarrow{b}$=（m，1），若向量$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$垂直，则m=7．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．若a＞1，则双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1的离心率的取值范围是（　　）
    A．（$\sqrt{2}$，+∞）B．（$\sqrt{2}$，2）C．（1，$\sqrt{2}$）D．（1，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．若x，y满足$\left\{\begin{array}{l}{x≤3}\\{x+y≥2}\\{y≤x}\end{array}\right.$，则x+2y的最大值为（　　）
    A．1B．3C．5D．9

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．下列说法中正确的是（　　）
    ①如果α是第一象限的角，则角-α是第四象限的角
    ②函数y=sinx在[-$\frac{π}{6}$，$\frac{2π}{3}$]上的值域是[-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$]
    ③已知角α的终边上的点P的坐标为（3，-4），则sinα=-$\frac{4}{5}$
    ④已知α为第二象限的角，化简tanα$\sqrt{1-{{sin}^2}α}$=sinα．
    A．①②B．①③C．③④D．②④

    查看答案和解析>>

    同步练习册答案