
分析 把ρ=1,ρ=2sin($\frac{π}{6}$-θ),分别化为直角坐标方程,两圆的方程相减可得经过两圆的交点的直线方程,求出圆心到直线的距离d,利用弦长公式即可得出.
解答 解:ρ=1,化为直角坐标方程:x2+y2=1.
ρ=2sin($\frac{π}{6}$-θ),展开可得:ρ2=2ρ$(\frac{1}{2}cosθ-\frac{\sqrt{3}}{2}sinθ)$,化为直角坐标方程:x2+y2=x-$\sqrt{3}$y.
两圆的方程相减可得经过两圆的交点的直线方程:x-$\sqrt{3}$y=1.
圆心O(0,0)到此直线的距离d=$\frac{1}{2}$.
∴|AB|=2$\sqrt{1-(\frac{1}{2})^{2}}$=$\sqrt{3}$.
点评 本题考查了极坐标与直角坐标方程的互化、点到直线的距离公式公式、直线与圆相减弦长公式,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
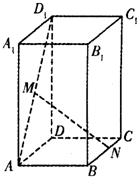 如图所示,侧棱与底面垂直,且底面为正方形的四棱柱ABCD-A1B1C1D1中,AA1=2,AB=1,M、N分别在AD1、BC上移动,始终保持MN∥平面DCC1D1,设BN=y,MN=x,则函数y=f(x)的图象大致是( )
如图所示,侧棱与底面垂直,且底面为正方形的四棱柱ABCD-A1B1C1D1中,AA1=2,AB=1,M、N分别在AD1、BC上移动,始终保持MN∥平面DCC1D1,设BN=y,MN=x,则函数y=f(x)的图象大致是( )| A. | 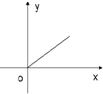 | B. | 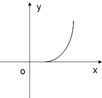 | C. | 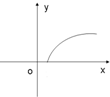 | D. | 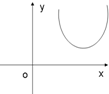 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f'(x)>0,g′(x)>0 | B. | f′(x)<0,g′(x)<0 | C. | f′(x)<0,g′(x)>0 | D. | f′(x)>0,g′(x)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com