
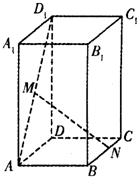
 如图所示,侧棱与底面垂直,且底面为正方形的四棱柱ABCD-A1B1C1D1中,AA1=2,AB=1,M、N分别在AD1、BC上移动,始终保持MN∥平面DCC1D1,设BN=y,MN=x,则函数y=f(x)的图象大致是( )
如图所示,侧棱与底面垂直,且底面为正方形的四棱柱ABCD-A1B1C1D1中,AA1=2,AB=1,M、N分别在AD1、BC上移动,始终保持MN∥平面DCC1D1,设BN=y,MN=x,则函数y=f(x)的图象大致是( )| A. | 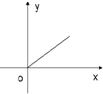 | B. | 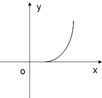 | C. | 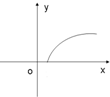 | D. | 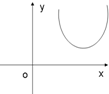 |
分析 由MN∥平面DCC1D1,过M点向AD做垂线,垂足为E,则ME=2AE=2BN,由此易得到函数y=f(x)的解析式,分析函数的性质,并逐一比照四个答案中的图象,得到函数的图象.
解答 解:MN∥平面DCC1D1,
则x=|MN|=$\sqrt{C{D}^{2}+(2BN)^{2}}=\sqrt{4{y}^{2}+1}$,
∴x2=4y2+1,即$y=\frac{1}{2}\sqrt{{x}^{2}-1}$.
即函数y=f(x)的解析式为
f(x)=$\frac{1}{2}\sqrt{{x}^{2}-1}$(x≥1).
其图象过(1,0)点,在区间[1,+∞)上呈凸状单调递增.
故选:C.
点评 本题考查的知识点是线面平行的性质,函数的图象与性质等,根据已知列出函数的解析式是解答本题的关键,是中档题.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2+2$\sqrt{3}$ | B. | 2+4$\sqrt{3}$ | C. | 4+4$\sqrt{3}$ | D. | 4+6$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>1 | B. | b>a>1 | C. | a<b<1 | D. | b<a<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 22 | C. | 24 | D. | 26 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com