解答:
(Ⅰ)解:函数f(x)的定义域为R,
f′(x)==,
∵a>0,
∴当x<-1,或x>1时,f′(x)<0;当-1<x<1时,f′(x)>0.
∴f(x)的单调递增区间为(-1,1),单调递减区间为(-∞,-1),(1,+∞).
(Ⅱ)证明:f(x)在区间(0,1)上单调递增,在区间(1,e)上单调递减,
又f(0)=2a,
f(e)=+2a>2a,
∴当x∈(0,e)时,f(x)>2a.
由g(x)=alnx-x+a,可得
g′(x)=-1=.
∴当a≥e时,函数g(x)在区间(0,e)上是增函数,
∴当x∈(0,e)时,g(x)<g(e)=2a-e<2a.
∴当x∈(0,e)时,
对于任意的x
1,x
2∈(0,e),都有f(x
1)>2a,g(x
2)<2a,∴f(x
1)>g(x
2).
当0<a<e时,函数g(x)在区间(0,a)上是增函数,在区间(a,e)上是减函数,
∴当x∈(0,e)时,g(x)≤g(a)=alna<2a.
∴当x∈(0,e)时,
对于任意的x
1,x
2∈(0,e),都有f(x
1)>2a,g(x
2)<2a,所以f(x
1)>g(x
2).
综上,对于任意的x
1,x
2∈(0,e),都有f(x
1)>g(x
2). …(13分)



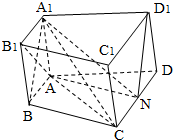 如图,在侧棱与底面垂直的四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥BC,且A1A=AB=BC=1,CD=2.
如图,在侧棱与底面垂直的四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥BC,且A1A=AB=BC=1,CD=2.