
分析 由题意可得a≥-b,b≥-a,由函数的单调性可得不等式,相加可得.
解答 证明:a+b≥0等价于a≥-b,b≥-a,
由函数f(x)为R上的增函数可得f(a)≥f(-a),f(b)≥f(-b),
由不等式的可加性可得f(a)+f(b)≥f(-a)+f(-b).
反之,若f(a)+f(b)≥f(-a)+f(-b),
可设a+b<0,等价于a<-b,b<-a,
由函数f(x)为R上的增函数可得f(a)<f(-b),f(b)<f(-a),
由不等式的可加性可得f(a)+f(b)<f(-a)+f(-b).
这与假设矛盾.则a+b≥0.
∴a+b≥0的充要条件是f(a)+f(b)≥f(-a)+f(-b).
点评 本题考查函数的单调性,涉及充要条件和不等式的性质,属基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
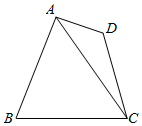 如图所示,在四边形ABCD中,已知BA⊥AD,AB=10,BC=5$\sqrt{6}$,∠BAC=60°,∠ADC=135°,CD=$\frac{5\sqrt{2}}{2}$.
如图所示,在四边形ABCD中,已知BA⊥AD,AB=10,BC=5$\sqrt{6}$,∠BAC=60°,∠ADC=135°,CD=$\frac{5\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com