
【题目】已知函数![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值域;
的值域;
(2)当![]() 时,求
时,求![]() 的最小值
的最小值![]() ;
;
(3)是否存在实数![]() 、
、![]() ,同时满足下列条件:①
,同时满足下列条件:① ![]() ;② 当
;② 当![]() 的定义域为
的定义域为![]() 时,其值域为
时,其值域为![]() .若存在,求出
.若存在,求出![]() 、
、![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1) ![]() (2)
(2)  (3) 不存在满足条件的实数
(3) 不存在满足条件的实数![]() 、
、![]() .见解析
.见解析
【解析】
(1)设t=3x,则φ(t)=t2﹣2at+3=(t﹣a)2+3﹣a2,φ(t)的对称轴为t=a,当a=1时,即可求出f(x)的值域;
(2)由函数φ(t)的对称轴为t=a,分类讨论当a![]() 时,当
时,当![]() a≤3时,当a>3时,求出最小值,则h(a)的表达式可求;
a≤3时,当a>3时,求出最小值,则h(a)的表达式可求;
(3)假设满足题意的m,n存在,函数h(a)在(3,+∞)上是减函数,求出h(a)的定义域,值域,然后列出不等式组,求解与已知矛盾,即可得到结论.
(1)当![]() 时,由
时,由![]() ,得
,得![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() .
.
(2)令![]() ,因为
,因为![]() ,故
,故![]() ,函数
,函数![]() 可化为
可化为
![]() .
.
① 当![]() 时,
时,![]() ;
;
② 当![]() 时,
时,![]() ;
;
③ 当![]() 时,
时,![]() .
.
综上,
(3)因为![]() ,
,![]() 为减函数,
为减函数,
所以![]() 在
在![]() 上的值域为
上的值域为![]() ,
,
又![]() 在
在![]() 上的值域为
上的值域为![]() ,所以,
,所以,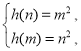 即
即
两式相减,得![]() ,
,
因为![]() ,所以
,所以![]() ,而由
,而由![]() 可得
可得![]() ,矛盾.
,矛盾.
所以,不存在满足条件的实数![]() 、
、![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,若对于
,若对于![]() 分别为某个三角形的边长,则称
分别为某个三角形的边长,则称![]() 为“三角形函数”.给出下列四个函数:
为“三角形函数”.给出下列四个函数:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中为“三角形函数”的个数是( )
.其中为“三角形函数”的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
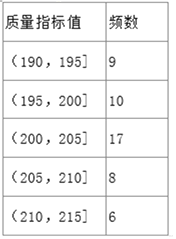
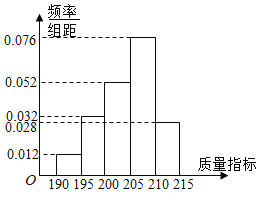
(1)根据频率分布直方图,估计乙流水线生产的产品该质量指标值的中位数;
(2)若将频率视为概率,某个月内甲、乙两条流水线均生产了5000件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
(3)根据已知条件完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
甲流水线 | 乙流水线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() ,其中
,其中![]() .
.
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() 分别是
分别是![]() 的中点将
的中点将![]() 分别沿
分别沿![]() 折起,使
折起,使![]() 重合于点
重合于点![]() .则下列结论正确的是( )
.则下列结论正确的是( )

A. ![]()
B. 平面![]()
C. 二面角![]() 的余弦值为
的余弦值为![]()
D. 点![]() 在平面
在平面![]() 上的投影是
上的投影是![]() 的外心
的外心
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市甲、乙两地为了争创“市级文明城市”,现市文明委对甲、乙两地各派10名专家进行打分评优,所得分数情况如下茎叶图所示.
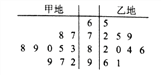
(1)分别计算甲、乙两地所得分数的平均值,并计算乙地得分的中位数;
(2)从乙地所得分数在![]() 间的成绩中随机抽取2份做进一步分析,求所抽取的成绩中,至少有一份分数在
间的成绩中随机抽取2份做进一步分析,求所抽取的成绩中,至少有一份分数在![]() 间的概率;
间的概率;
(3)在甲、乙两地所得分数超过90分的成绩中抽取其中2份分析其合理性,求这2份成绩都是来自甲地的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数 被称为狄利克雷函数,其中
被称为狄利克雷函数,其中![]() 为实数集,
为实数集,![]() 为有理数集,则关于函数
为有理数集,则关于函数![]() 有如下四个命题:①
有如下四个命题:①![]() ;②函数
;②函数![]() 是偶函数;③任取一个不为零的有理数
是偶函数;③任取一个不为零的有理数![]() ,
,![]() 对任意的
对任意的![]() 恒成立;④存在三个点
恒成立;④存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等边三角形.其中真命题的个数有( )
为等边三角形.其中真命题的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.

(1)用分段函数的形式表示函数![]() 的解析式,并画出
的解析式,并画出![]() 在
在![]() 上的大致图像;
上的大致图像;
(2)若关于x的方程![]() 恰有一个实数解,求出实数m的取值范围组成的集合;
恰有一个实数解,求出实数m的取值范围组成的集合;
(3)当![]() 时,求函数
时,求函数![]() 的值域.
的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com