
| A. | 1 | B. | $\sqrt{2}$ | C. | ln2 | D. | $\sqrt{2}$ln2 |
分析 此题要求的虽然是绝对值的最小值,但是通过观察发现两个方程都是非μ常规的我们不会解的方程类型,所以我们换个思路,运用函数的思想来解决方程的有关问题.将方程的解x1看作是函数y1=ex与函数y0=a-x交点坐标的横坐标值;将方程的解x2看作是函数y2=lnx与函数y0=a-x交点坐标值得横坐标;由于函数y1,y2互为反函数,均与直线y0有交点,所以两个交点关于直线y=x对称,所以x2=${e}^{{x}_{1}}$,|x1-x2|=|${e}^{{x}_{1}}$-x1|,可看作是函数g(x)=ex-x的绝对值,此时问题变为求函数绝对值的最小值,又因为其为非常规函数,所以应用导数的方法求解.
解答 解:方程ex+x=a的解x1可以看作是函数y1=ex与函数y0=a-x交点坐标的横坐标值;
方程lnx+x=a的解x2可以看作是函数y2=lnx与函数y0=a-x交点坐标的横坐标值;
∵函数y1,y2互为反函数,且均与函数y0有交点,
∴两个交点关于直线y=x对称,∴x2=${e}^{{x}_{1}}$,
∴|x1-x2|=|${e}^{{x}_{1}}$-x1|,
构造函数g(x)=ex-x,则丨x1-x2丨的最小值可以看作函数丨g(x)丨的最小值;
我们用导数的方法一研究其何时取得最小值;
∴函数g(x)=ex-x的导数g′(x)=ex-1,则g′(x)=0的解为x=0;
∴|x1-x2|=|${e}^{{x}_{1}}$-x1|=|g(x)|,故其最小值为1;
故选:A.
点评 这道题充分利用了函数的性质,互逆函数间的对称关系,并利用导数的方法研究函数的最值问题.难点在于将方程的解变成是函数的交点,并采用构造函数的方法研究最值问题.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | -6 | C. | 6 | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
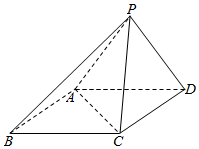 已知四棱锥P-ABCD的底面ABCD是菱形,∠ABC=60°,AB=PC=2,$PA=PD=\sqrt{2}$.
已知四棱锥P-ABCD的底面ABCD是菱形,∠ABC=60°,AB=PC=2,$PA=PD=\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
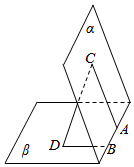 如图,在二面角α-AB-β中,线段AC?α,BD?β,AC⊥AB,BD⊥AB,AC=CD=4,AB=BD=2,则二面角α-AB-β的大小为$\frac{π}{3}$.
如图,在二面角α-AB-β中,线段AC?α,BD?β,AC⊥AB,BD⊥AB,AC=CD=4,AB=BD=2,则二面角α-AB-β的大小为$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
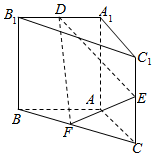 直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,E,F分别是CC1,BC的中点,AE⊥A1B1,D为棱A1B1上的点.
直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,E,F分别是CC1,BC的中点,AE⊥A1B1,D为棱A1B1上的点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
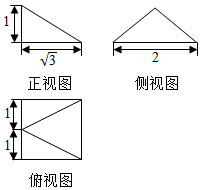
| A. | $3+\sqrt{3}$ | B. | $3+\sqrt{6}$ | C. | $1+2\sqrt{3}$ | D. | $1+2\sqrt{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com