
| A. | $\frac{3}{2}$ | B. | -6 | C. | 6 | D. | -$\frac{3}{2}$ |
分析 直接由复数代数形式的乘除运算化简复数$\frac{a+3i}{1-2i}$,又已知复数$\frac{a+3i}{1-2i}$是实数,则虚部等于0,求解即可得实数a的值.
解答 解:$\frac{a+3i}{1-2i}$=$\frac{(a+3i)(1+2i)}{(1-2i)(1+2i)}=\frac{a-6+(2a+3)i}{5}$=$\frac{a-6}{5}+\frac{2a+3}{5}i$,
又∵复数$\frac{a+3i}{1-2i}$是实数,
∴$\frac{2a+3}{5}=0$,解得a=$-\frac{3}{2}$.
故选:D.
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
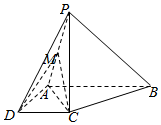 如图,在四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥DC,AD⊥CD,PC⊥平面ABCD.
如图,在四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥DC,AD⊥CD,PC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{15}{16}$ | B. | -$\frac{27}{16}$ | C. | $\frac{8}{9}$ | D. | -$\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | ln2 | D. | $\sqrt{2}$ln2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (理科)四棱镜P-ABCD中,PD⊥平面ABCD,2AD=AB=BC=2a,AD∥BC,PD=$\sqrt{3}$a,∠DAB=60°.
(理科)四棱镜P-ABCD中,PD⊥平面ABCD,2AD=AB=BC=2a,AD∥BC,PD=$\sqrt{3}$a,∠DAB=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com