
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{9}$ | D. | $\frac{7}{9}$ |
分析 根据题意,利用随机事件的概率公式,分别求出事件A的概率与事件A、B同时发生的概率,再用条件概率公式加以计算,可得P(B|A)的值.
解答 解:根据题意,若事件A为“x+y为偶数”发生,则x、y两个数均为奇数或均为偶数.
共有2×3×3=18个基本事件,
∴P(A)=$\frac{18}{36}$=$\frac{1}{2}$,
而A、B同时发生,基本事件有当一共有9个基本事件,
P(AB)=$\frac{9}{36}$=$\frac{1}{4}$,
因此,在事件A发生的情况下,B发生的概率为P(B|A)=$\frac{\frac{1}{4}}{\frac{1}{2}}$=$\frac{1}{2}$.
故选:B.
点评 本题给出掷骰子的事件,求条件概率.着重考查了随机事件的概率公式、条件概率的计算等知识,属于中档题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{3}$-y2=1 | B. | $\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{4}$=1 | C. | x2-$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{8}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | -6 | C. | 6 | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
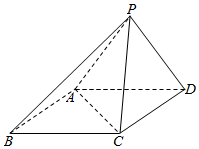 已知四棱锥P-ABCD的底面ABCD是菱形,∠ABC=60°,AB=PC=2,$PA=PD=\sqrt{2}$.
已知四棱锥P-ABCD的底面ABCD是菱形,∠ABC=60°,AB=PC=2,$PA=PD=\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com