
分析 (1)先排好5个空座位,再把这5人,插入5个空座位所成为的6个空位中的5个,问题得以解决,
(2)先把2个空座位排在甲乙之间,并捆绑在一起看做一个复合元素和在另外3人,从8个位置中任选4个,问题得以解决,
(3)甲和乙的顺序只有两种,求出所有坐法乘以$\frac{1}{2}$,问题得以解决.
解答 解:(1)先排好5个空座位,再把这5人,插入5个空座位所成为的6个空位中的5个,故有A65=600种,
(2)先把2个空座位排在甲乙之间,并捆绑在一起看做一个复合元素和在另外3人,从8个位置中任选4个,故有A22A84=3360种,
(3)甲和乙的顺序只有两种,故甲必须坐在乙的左边的坐法有$\frac{1}{2}$A105=15120种.
点评 本题主要考查了排列问题中的相邻和不相邻的问题,相邻用捆绑,不相邻用插空,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)为对数函数 | B. | f(x)为幂函数 | C. | f(x)为指数函数 | D. | f(x)为正比例函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
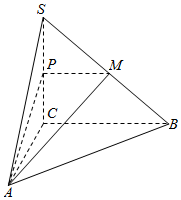 如图,在三棱锥S-ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°.
如图,在三棱锥S-ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com