
分析 (Ⅰ)根据函数的对称轴求出b的值,根据函数的最小值求出c的值,从而求出函数的解析式即可;
(Ⅱ)分别求出|AB|-|CD|,|CB|,得到不等式(2+$\sqrt{2}$)$\sqrt{1-t}$<$\sqrt{2}$$\sqrt{1+t}$,解出即可.
解答 解:(Ⅰ)∵f(1+x)=f(1-x),
∴函数的对称轴是x=1,即-$\frac{b}{2}$=1,解得:b=-2;
∵f(x)的最小值是-1,∴$\frac{4c{-b}^{2}}{4}$=-1,解得:c=0,
∴f(x)=x2-2x;
(Ⅱ)若函数y=|f(x)|与y=t相交于4个不同交点,则0<t<1,
易知xA=1-$\sqrt{1+t}$,xB=1-$\sqrt{1-t}$,xC=1+$\sqrt{1-t}$,xD=1+$\sqrt{1+t}$,
∴|AB|-|CD|=$\sqrt{1+t}$-$\sqrt{1-t}$,|CB|=2$\sqrt{1-t}$,
∴线段|AB|,|BC|,|CD|能构成等腰锐角三角形,
∴|BC|≤$\sqrt{2}$|AB|,即2$\sqrt{1-t}$<$\sqrt{2}$($\sqrt{1+t}$-$\sqrt{1-t}$),
即(2+$\sqrt{2}$)$\sqrt{1-t}$<$\sqrt{2}$•$\sqrt{1+t}$,
解得:$\frac{\sqrt{2}}{2}$<t<1.
点评 本题考查了求二次函数的表达式,考查不等式问题,是一道中档题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
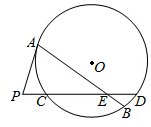 如图,圆O的弦AB,CD相交于点E,过点A作圆O的切线与DC的延长线交于点P,若PA=6,AE=9,BE=2,ED=3,则PC=( )
如图,圆O的弦AB,CD相交于点E,过点A作圆O的切线与DC的延长线交于点P,若PA=6,AE=9,BE=2,ED=3,则PC=( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com