
分析 (I)$\frac{a-c}{a-b}$=$\frac{sin(A+C)}{sinA+sinC}$,由正弦定理可得:$\frac{a-c}{a-b}$=$\frac{sin(A+C)}{sinA+sinC}$=$\frac{sinB}{sinA+sinC}$=$\frac{b}{a+c}$,化简利用余弦定理即可得出.(Ⅱ)取 BC中点D,则$|{\overrightarrow{C{A}}-\frac{1}{2}\overrightarrow{C{B}}}|=2=|{\overrightarrow{D{A}}}|$,在△ADC中,AD2=AC2+CD2-2 AC•CDcosC,化简利用基本不等式的性质与三角形面积计算公式即可得出.
解答 解:(I)∵$\frac{a-c}{a-b}$=$\frac{sin(A+C)}{sinA+sinC}$,由正弦定理可得:$\frac{a-c}{a-b}$=$\frac{sin(A+C)}{sinA+sinC}$=$\frac{sinB}{sinA+sinC}$=$\frac{b}{a+c}$,化为:a2-c2=ab-b2,
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{1}{2}$,C∈(0,π).
∴$C=\frac{π}{3}$.
(Ⅱ)取 BC中点D,则$|{\overrightarrow{C{A}}-\frac{1}{2}\overrightarrow{C{B}}}|=2=|{\overrightarrow{D{A}}}|$,
在△ADC中,AD2=AC2+CD2-2 AC•CDcosC,
即$4={b^2}+{({\frac{a}{2}})^2}-\frac{ab}{2}$$≥2\sqrt{\frac{{{a^2}{b^2}}}{4}}-\frac{ab}{2}=\frac{ab}{2}$,
∴ab≤8,当且仅当a=4,b=2时取等号.
此时${S_{△{A}{B}C}}=\frac{1}{2}absinC=\frac{{\sqrt{3}}}{4}ab$,其最大值为$2\sqrt{3}$.
点评 本题考查了三角形面积计算公式、正弦定理余弦定理、数量积运算性质、基本不等式的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$-cos1 | B. | $\frac{{π}^{2}}{2}$+1 | C. | π | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
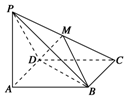 如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,请你补充一个条件①(或③),使平面MBD⊥平面PCD.①DM⊥PC ②DM⊥BM③BM⊥PC ④PM=MC(填写你认为是正确的条件对应的序号).
如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,请你补充一个条件①(或③),使平面MBD⊥平面PCD.①DM⊥PC ②DM⊥BM③BM⊥PC ④PM=MC(填写你认为是正确的条件对应的序号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com