
分析 直接利用三角函数的诱导公式对(1)(2)化简求值.
解答 解:(1)$\frac{-sin(180°+α)+sin(-α)-tan(360°+α)}{tan(α+180°)+cos(-α)+cos(180°-α)}$
=$\frac{-(-sinα)-sinα-tanα}{tanα+cosα-cosα}$=$\frac{-tanα}{tanα}=-1$;
(2)$\frac{{cos({α-\frac{π}{2}})}}{{sin({\frac{5π}{2}+α})}}•sin({π-α})•cos({2π+α})$
=$\frac{sinα}{cosα}$•sinα•cosα=sin2α.
点评 本题考查三角函数的化简求值,考查了诱导公式的应用,是基础的计算题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{5}-2$ | C. | $\sqrt{5}+2$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
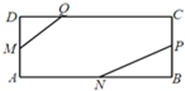 如图在长方形ABCD中,已知AB=4,BC=2,M,N,P为长方形边上的中点,Q是边CD上的点,且CQ=3DQ,求 $\overrightarrow{MQ}$•$\overrightarrow{NP}$的值.
如图在长方形ABCD中,已知AB=4,BC=2,M,N,P为长方形边上的中点,Q是边CD上的点,且CQ=3DQ,求 $\overrightarrow{MQ}$•$\overrightarrow{NP}$的值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+$\frac{1}{a}$>b+$\frac{1}{b}$ | B. | a+$\frac{1}{b}$>b+$\frac{1}{a}$ | C. | $\frac{b}{a}$>$\frac{b+1}{a+1}$ | D. | $\frac{2a-b}{a+2b}$>$\frac{a}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com