Question

17．已知椭圆的方程是$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1，以椭圆的长轴为直径作圆，若直线x=x₀与圆和椭圆在x轴上方的部分分别交于P，Q两点，则△POQ的面积S_△POQ的最大值为（　　）

• A． $\frac{3}{2}$
• B． $\frac{1}{4}$
• C． $\frac{3}{4}$
• D． $\frac{1}{2}$

Answer 1

分析 由题意画出图形，设出P，Q的坐标，求得|PQ|=$\frac{1}{3}\sqrt{9-{{x}_{0}}^{2}}$，代入三角形的面积后利用基本不等式求得最值．

解答 解：如图，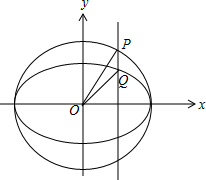

由题意可设P（${x}_{0}，\sqrt{9-{{x}_{0}}^{2}}$），Q（${x}_{0}，\frac{2}{3}\sqrt{9-{{x}_{0}}^{2}}$），
∴|PQ|=$\frac{1}{3}\sqrt{9-{{x}_{0}}^{2}}$，
则${S}_{△POQ}=\frac{1}{2}{x}_{0}•\frac{1}{3}\sqrt{9-{{x}_{0}}^{2}}$=$\frac{1}{6}\sqrt{{{x}_{0}}^{2}（9-{{x}_{0}}^{2}）}$$≤\frac{1}{6}\sqrt{（\frac{{{x}_{0}}^{2}+9-{{x}_{0}}^{2}}{2}）^{2}}=\frac{1}{6}×\frac{9}{2}=\frac{3}{4}$．
上式当且仅当${{x}_{0}}^{2}=9-{{x}_{0}}^{2}$，即${x}_{0}=±\frac{3\sqrt{2}}{2}$时取“=”，
∴△POQ的面积S_△POQ的最大值为$\frac{3}{4}$．
故选：C．

点评 本题考查椭圆的简单性质，考查了利用基本不等式求函数的最值，是中档题．