
已知数列 的前
的前 项和为
项和为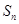 ,且
,且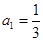 ,
,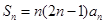
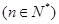 .
.
(1)求 的值;
的值;
(2)猜想 的通项公式,并用数学归纳法证明.
的通项公式,并用数学归纳法证明.
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:解答题
观察数表
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10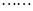
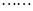
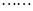
求:(1)这个表的第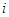 行里的最后一个数字是多少?
行里的最后一个数字是多少?
(2)第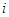 行各数字之和是多少?
行各数字之和是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
设数列{an}的前n项和为Sn=2n2,{bn}为等比数列,且a1=b1,b2(a2-a1)=b1.
(1)求数列{an}和{bn}的通项公式;
(2)设cn=,求数列{cn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com