
| A. | $({\frac{1}{e},+∞})$ | B. | (1,+∞) | C. | (1,2) | D. | (2,+∞) |
分析 求出函数的导数,问题转化为f′(x)在($\frac{1}{2}$,1)先大于0,再小于0,得到关于a的不等式组,解出即可.
解答 解:f′(x)=ax-(1+2a)+$\frac{2}{x}$=$\frac{{ax}^{2}-(2a+1)x+2}{x}$,(a>0,x>0)
若f(x)在($\frac{1}{2}$,1)有极大值,
则f′(x)在($\frac{1}{2}$,1)先大于0,再小于0,
则$\left\{\begin{array}{l}{f′(\frac{1}{2})>0}\\{f′(1)<0}\end{array}\right.$,解得:1<a<2,
故选:C.
点评 本题考查了函数的单调性、极值的意义,考查不等式以及二次函数的性质,是一道中档题.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
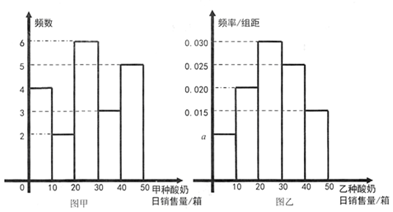
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\sqrt{2}})$ | B. | $({-∞,\sqrt{2}})$ | C. | $({-∞,2\sqrt{2}})$ | D. | $({-2\sqrt{2},\frac{{\sqrt{2}}}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
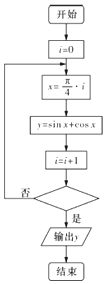
| A. | i>5? | B. | i>3? | C. | i>6? | D. | i>4? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{5}$-i | B. | $\sqrt{5}$-i | C. | i | D. | -i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | 9 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p是假命题,¬p::?x∈(0,$\frac{π}{2}}$),f(x)≥0 | B. | p是假命题,¬p::?x∈(0,$\frac{π}{2}}$),f(x)≥0 | ||
| C. | P是真命题,¬p::?x∈(0,$\frac{π}{2}}$),f(x)≥0 | D. | p是真命题,¬p::?x∈(0,$\frac{π}{2}}$),f(x)≥0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com