
分析 (1)直接利用复数代数形式的乘除运算化简得答案;
(2)把z代入az+b=1-i,然后利用复数相等的条件列式求得实数a,b的值.
解答 解:(1)$z=\frac{{{{(1-i)}^2}-3(1+i)}}{2-i}$=$\frac{-3-5i}{2-i}=\frac{(-3-5i)(2+i)}{(2-i)(2+i)}$=$-\frac{1}{5}-\frac{13}{5}i$;
(2)由az+b=1-i,得$a(-\frac{1}{5}-\frac{13}{5}i)+b=1-i$,
即$-\frac{a}{5}+b-\frac{13a}{5}i=1-i$,
∴$\left\{\begin{array}{l}{-\frac{a}{5}+b=1}\\{-\frac{13a}{5}=-1}\end{array}\right.$,解得$a=\frac{5}{13},b=\frac{14}{13}$.
点评 本题考查复数代数形式的乘除运算,考查复数相等的条件,是基础题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 若l⊥β,则 α⊥β | B. | 若α⊥β,则l⊥m | C. | 若l∥β,则α∥β | D. | 若α∥β,则l∥m |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
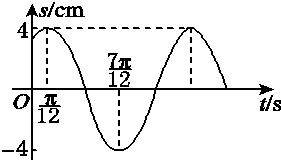 如图所示,弹簧上挂的小球做上下振动时,小球离开平衡位置的距离s(cm)随时间t(s)的变化曲线是一个三角函数的图象.
如图所示,弹簧上挂的小球做上下振动时,小球离开平衡位置的距离s(cm)随时间t(s)的变化曲线是一个三角函数的图象.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,±\sqrt{m-n})$ | B. | $(±\sqrt{m-n},0)$ | C. | $(0,±\sqrt{n-m})$ | D. | $(±\sqrt{n-m},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com