
【题目】如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ
(1)试将由A到C所用的时间t表示为θ的函数t(θ);
(2)问θ为多少时,由A到C所用的时间t最少?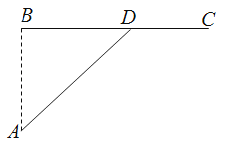
科目:高中数学 来源: 题型:
【题目】近几年出现各种食品问题,食品添加剂会引起血脂增高、血压增高、血糖增高等疾病.为了解三高疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
患三高疾病 | 不患三高疾病 | 合计 | |
男 | 6 | 30 | |
女 | |||
合计 | 36 |
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式 ![]() ,其中
,其中 ![]() )
)
(1)请将如图的列联表补充完整;若用分层抽样的方法在患三高疾病的人群中抽 ![]() 人,其中女性抽多少人?
人,其中女性抽多少人?
(2)为了研究三高疾病是否与性别有关,请计算出统计量 ![]() ,并说明你有多大的把握认为三高疾病与性别有关?
,并说明你有多大的把握认为三高疾病与性别有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+1(a,b为实数),x∈R, ![]()
(1)若f(﹣1)=0,且函数f(x)的值域为[0,+∞),求F(x)的表达式;
(2)在(1)的条件下,当x∈[﹣2,2]时,g(x)=f(x)﹣kx是单调函数,求实数k的取值范围;
(3)设mn<0,m+n>0,a>0且f(x)为偶函数,判断F(m)+F(n)能否大于零.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
参考公式及数据: 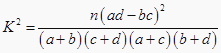
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中, ![]() 点
点![]() 是
是![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,连接
,连接![]() 得到如图
得到如图![]() 所示的几何体.
所示的几何体.

(1)求证; ![]() 平面
平面![]() ;
;
(2)若![]() 二面角
二面角![]() 的平面角的正切值为
的平面角的正切值为![]() 求二面角
求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点P在☉O外,PC是☉O的切线,切点为C,直线PO与☉O相交于点A,B. 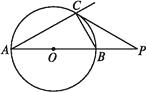
(1)试探索∠BCP与∠P的数量关系;
(2)若∠A=30°,则PB与PA有什么关系?
(3)∠A可能等于45°吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com