
| �ſ� | ���ſ� | �ϼ� | |
| ���� | 26 | 24 | 50 |
| �� | 30 | 20 | 50 |
| �ϼ� | 56 | 44 | 100 |
| P��K2��k0�� | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
���� ��1��������������K2�������ٽ�ֵ�����ɵó����ۣ�
��2������������ȡ��5λŮ���С��ſء���3�ˣ���X�����п���ȡֵ��
�����Ӧ�ĸ��ʣ�д��X �ķֲ��У�������ѧ����ֵ��
��� �⣺��1������������֪��
${K^2}=\frac{{n{{��ad-bc��}^2}}}{��a+b����c+d����a+c����b+d��}$=$\frac{100{����26��20-30��24��}^{2}}{56��44��50��50}$=$\frac{50}{77}$��0.649��
��0.649��0.708��
��û��60%�İ�����Ϊ���ſء��롱�Ա��йأ�
��2��������֪������ȡ��5λŮ���С��ſء���3�ˣ�
�����ſء���2�ˣ�
��X�����п���ȡֵΪ1��2��3��
��P��X=1��=$\frac{{C}_{3}^{1}{•C}_{2}^{2}}{{C}_{5}^{3}}$=$\frac{3}{10}$��P��X=2��=$\frac{{C}_{3}^{2}{•C}_{2}^{1}}{{C}_{5}^{3}}$=$\frac{3}{5}$��P��X=3��=$\frac{{C}_{3}^{3}}{{C}_{5}^{3}}$=$\frac{1}{10}$��
��X �ķֲ���Ϊ��
| X | 1 | 2 | 3 |
| P��X�� | $\frac{3}{10}$ | $\frac{3}{5}$ | $\frac{1}{10}$ |
���� ���⿼���˶����Լ�������������ķֲ��к���ѧ�����ļ������⣬�ǻ�����Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-3��0�� | B�� | ��-2��0�� | C�� | ��-3��-2�� | D�� | ��0��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30�� | B�� | 30���150�� | C�� | 60�� | D�� | 60���120�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
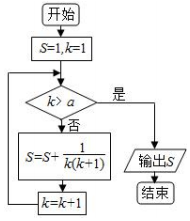
| A�� | a=11 | B�� | a=12 | C�� | a=13 | D�� | a=14 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{6}$ | B�� | $\frac{��}{3}$ | C�� | $\frac{2��}{3}$ | D�� | $\frac{5��}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | -9 | C�� | 22 | D�� | 21 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com