
 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,AB∥CD,AB=BC=$\frac{1}{2}$CD,E为AA1的中点.
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,AB∥CD,AB=BC=$\frac{1}{2}$CD,E为AA1的中点.分析 (1)取CD的中点G,DD1的中点F,连接BG,FG,EF.依次证明四边形ABGD,四边形ADFE,四边形BGFE是平行四边形,得出BE∥FG,结合FG∥CD1得出结论;
(2)利用勾股定理逆定理证明BE⊥B1E,利用等腰三角形性质得出BC⊥CD,从而可证BC⊥平面ABE,得出BE⊥BC即BE⊥B1C1,从而有BE⊥平面EB1C1,故平面EB1C1⊥平面EBC.
解答 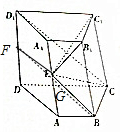 证明:(1)取CD的中点G,DD1的中点F,连接BG,FG,EF.
证明:(1)取CD的中点G,DD1的中点F,连接BG,FG,EF.
则FG∥CD1,
∵AB∥CD,AB=$\frac{1}{2}$CD=DG,
∴四边形ABGD是平行四边形,
∴AD∥BG,AD=BG.
∵E是DD1的中点,F是AA1的中点,AA1∥DD1,AA1=DD1,
∴DF∥AE,DF=AE,
∴四边形AEFD是平行四边形,
∴EF∥AD,EF=AD,
∴EF∥BG,EF=BG,
∴四边形BEFG是平行四边形,
∴BE∥FG,又FG∥CD1,
∴BE∥CD1.
(2)∵CG=$\frac{1}{2}$CD=BC,∠BGC=∠ADC=45°,
∴∠BCD=90°,即BC⊥CD,
又AB∥CD,∴BC⊥AB,
∵AA1⊥平面ABCD,BC?平面ABCD,
∴AA1⊥BC,又AB∩AA1=A,
∴BC⊥平面ABE,又BE?平面ABE,
∴BC⊥BE,又BC∥B1C1,
∴BE⊥B1C1.
设AB=1,则A1B1=1,AA1=BB1=CC1=CD=2,
∴AE=A1E=$\frac{1}{2}A{A}_{1}$=1,BE=B1E=$\sqrt{2}$,
∴BE2+B1E2=BB12,∴BE⊥B1E,
又B1E∩B1C1=B1,B1E?平面EB1C1,B1C1?平面EB1C1,
∴BE⊥平面EB1C1,又BE?平面EBC,
∴平面EB1C1⊥平面EBC.
点评 本题考查了面面垂直的判定定理,线面垂直的性质,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 在直角梯形ABCD中,AB∥DC,AD⊥AB,AD=AB=2DC=2,点E、F分别在线段DC、AB上,设$\overrightarrow{DE}$=λ$\overrightarrow{DC}$,$\overrightarrow{AF}$=λ$\overrightarrow{AB}$,则$\overrightarrow{AE}$•$\overrightarrow{CF}$的最小值为-$\frac{33}{8}$.
在直角梯形ABCD中,AB∥DC,AD⊥AB,AD=AB=2DC=2,点E、F分别在线段DC、AB上,设$\overrightarrow{DE}$=λ$\overrightarrow{DC}$,$\overrightarrow{AF}$=λ$\overrightarrow{AB}$,则$\overrightarrow{AE}$•$\overrightarrow{CF}$的最小值为-$\frac{33}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
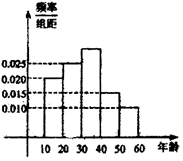 某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,远离毒品”的电视公益广告,期望让更多的市民知道毒品的危害性.禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.
某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,远离毒品”的电视公益广告,期望让更多的市民知道毒品的危害性.禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com