
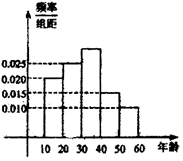
 某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,远离毒品”的电视公益广告,期望让更多的市民知道毒品的危害性.禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.
某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,远离毒品”的电视公益广告,期望让更多的市民知道毒品的危害性.禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.分析 (Ⅰ)先求出随机抽取的市民中年龄段在[30,40)的频率,由此能求出随机抽取的市民中年龄段在[30,40)的人数.
(Ⅱ)年龄段在[40,50),[50,60)的人数分别为15人,10人,从而不小于40岁的人的频数是25人,由此能示出在[50,60)年龄段抽取的人数.
(Ⅲ)由已知X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(Ⅰ)由图知,随机抽取的市民中年龄段在[30,40)的频率为:
1-10(0.020+0.025+0.015+0.010)=0.3,
∴随机抽取的市民中年龄段在[30,40)的人数为100×0.3=30人.
(Ⅱ)由(1)知:年龄段在[40,50),[50,60)的人数分别为100×0.15=15人,100×0.1=10人,
即不小于40岁的人的频数是25人,
所以在[50,60)年龄段抽取的人数为10×$\frac{5}{25}$=2人.
(Ⅲ)由已知X的可能取值为0,1,2,
P(X=0)=$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$=$\frac{3}{10}$,
P(X=1)=$\frac{{C}_{2}^{1}{C}_{3}^{1}}{{C}_{5}^{2}}$=$\frac{3}{5}$,
P(X=2)=$\frac{{C}_{2}^{2}}{{C}_{5}^{2}}$=$\frac{1}{10}$,
所以X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{3}{10}$ | $\frac{3}{5}$ | $\frac{1}{10}$ |
点评 本题考查频率分布直方图的应用,考查分层抽样的应用,考查离散型随机变量的分布列及数学期望的求法,是中档题,在历年高考中都是必考题型之一.


科目:高中数学 来源: 题型:选择题
| A. | 8x-6y-21=0 | B. | 8x+6y-21=0 | C. | 6x+8y-21=0 | D. | 6x-8y-21=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,AB∥CD,AB=BC=$\frac{1}{2}$CD,E为AA1的中点.
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,AB∥CD,AB=BC=$\frac{1}{2}$CD,E为AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2-\sqrt{2}}{2}$ | C. | $\frac{3-\sqrt{3}}{3}$ | D. | $\frac{2-\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$∥$\overrightarrow{b}$ | B. | $\overrightarrow{a}$+2$\overrightarrow{b}$=0 | C. | $\frac{\overrightarrow{a}}{|\overrightarrow{a}|}$+$\frac{\overrightarrow{b}}{|\overrightarrow{b}|}$=0 | D. | 2$\overrightarrow{a}$+$\overrightarrow{b}$=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com