
【题目】已知函数![]() .
.
(1)当![]() 时,求函数的值域;
时,求函数的值域;
(2)若函数![]() 的最大值是
的最大值是![]() ,求
,求![]() 的值;
的值;
(3)已知![]() ,若存在两个不同的正数
,若存在两个不同的正数![]() ,当函数
,当函数![]() 的定义域为
的定义域为![]() 时,
时,![]() 的值域为
的值域为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)![]() 时写出函数表达式,根据真数范围求解函数值域即可。(2)设
时写出函数表达式,根据真数范围求解函数值域即可。(2)设![]() 换元真数部分为关于
换元真数部分为关于![]() 的一元二次函数,又
的一元二次函数,又![]() 有最大值,所以开口只能向下,即
有最大值,所以开口只能向下,即![]() ,在对称轴处取得最大值,即可求出
,在对称轴处取得最大值,即可求出![]() 的范围。(3)较易判断
的范围。(3)较易判断![]() 为增函数,函数
为增函数,函数![]() 的定义域为
的定义域为![]() 时,
时,![]() 的值域为
的值域为![]() 可理解为函数
可理解为函数![]() 与
与![]() 有两个交点正数交点
有两个交点正数交点![]() ,
,![]() ,另外将
,另外将![]() 进行换元即可转化成关于
进行换元即可转化成关于![]() 的一个一元二次函数求解。
的一个一元二次函数求解。
(1)![]() 时,
时,![]()
因为![]() ,所以
,所以![]()
所以此时![]() 的值域是
的值域是![]() 。
。
(2)设![]()
![]() ,则
,则![]() ,若此时
,若此时![]() ,开口向上没有最大值。由第一问可知)
,开口向上没有最大值。由第一问可知)![]() 时也不满足,所以开口只能向下,即
时也不满足,所以开口只能向下,即![]() 且此时对称轴
且此时对称轴![]() 。
。
当![]() 时,最大值在对称轴处取得,
时,最大值在对称轴处取得,
即![]()
解出![]() 或
或![]() (舍)
(舍)
所以![]() 。
。
(3)当![]() 时,设
时,设![]() ,设真数为
,设真数为![]() ,此时对称轴
,此时对称轴![]() ,所以当
,所以当![]() 时m为增函数,即
时m为增函数,即![]() 为增函数。
为增函数。
所以函数![]() 的定义域为
的定义域为![]() 时,
时,![]() 的值域为
的值域为![]() ,可理解为函数
,可理解为函数![]() 与
与![]() 有两个交点正数交点
有两个交点正数交点![]() ,
,![]() ,
,
即![]() 有两个正根。
有两个正根。
即![]() ,设
,设![]()
所以![]()
即![]() 有两个大于1的根。
有两个大于1的根。
所以此时只需![]() 即可,即
即可,即![]()
又![]() ,所以
,所以![]() 。
。


科目:高中数学 来源: 题型:
【题目】在一次社会实践活动中,某数学调研小组根据车间持续5个小时的生产情况画出了某种产品的总产量![]() (单位:千克)与时间
(单位:千克)与时间![]() (单位:小时)的函数图像,则以下关于该产品生产状况的正确判断是( ).
(单位:小时)的函数图像,则以下关于该产品生产状况的正确判断是( ).
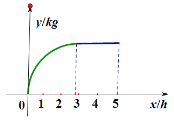
A.在前三小时内,每小时的产量逐步增加
B.在前三小时内,每小时的产量逐步减少
C.最后一小时内的产量与第三小时内的产量相同
D.最后两小时内,该车间没有生产该产品
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,曲线C1的参数方程为![]() 以原点O为极点,x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为
以原点O为极点,x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为![]()
(1)求曲线C1与C2的直角坐标方程;
(2)当C1与C2有两个公共点时,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一次全市高中男生身高统计调查数据显示:全市![]() 名男生的身高服从正态分布
名男生的身高服从正态分布![]() .现从某学校高三年级男生中随机抽取
.现从某学校高三年级男生中随机抽取![]() 名测量身高,测量发现被测学生身高全部介于
名测量身高,测量发现被测学生身高全部介于![]() 和
和![]() 之间,将测量结果按如下方式分组:
之间,将测量结果按如下方式分组: ![]() ,
, ![]() ,…,
,…, ![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(Ⅰ)试评估该校高三年级男生在全市高中男生中的平均身高状况;
(Ⅱ)求这![]() 名男生身高在
名男生身高在![]() 以上(含
以上(含![]() )的人数;
)的人数;
(Ⅲ)在这![]() 名男生身高在
名男生身高在![]() 以上(含
以上(含![]() )的人中任意抽取
)的人中任意抽取![]() 人,该
人,该![]() 人中身高排名(从高到低)在全市前
人中身高排名(从高到低)在全市前![]() 名的人数记力
名的人数记力![]() ,求
,求![]() 的数学期望.
的数学期望.
参考数据:若![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com