
【题目】下列四个结论中,错误的序号是___________.①以直角坐标系中![]() 轴的正半轴为极轴的极坐标系中,曲线C的方程为
轴的正半轴为极轴的极坐标系中,曲线C的方程为![]() ,若曲线C上总存在两个点到原点的距离为
,若曲线C上总存在两个点到原点的距离为![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() ;②在残差图中,残差点比较均匀地落在水平带状区域中,说明选用的模型比较合适,这样的带状区域宽度越宽,说明模型拟合精度越高;③设随机变量
;②在残差图中,残差点比较均匀地落在水平带状区域中,说明选用的模型比较合适,这样的带状区域宽度越宽,说明模型拟合精度越高;③设随机变量![]() ,若
,若![]() ,则
,则![]() ;④已知
;④已知![]() 为满足
为满足![]() 能被9整除的正数
能被9整除的正数![]() 的最小值,则
的最小值,则![]() 的展开式中,系数最大的项为第6项.
的展开式中,系数最大的项为第6项.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】土笋冻是闽南种广受欢迎的特色传统风味小吃某小区超市销售一款土笋冻,进价为每个15元,售价为每个20元.销售的方案是当天进货,当天销售,未售出的全部由厂家以每个10元的价格回购处理.根据该小区以往的销售情况,得到如图所示的频率分布直方图:

(1)估算该小区土笋冻日需求量的平均数![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)已知该超市某天购进了150个土笋冻,假设当天的需求量为![]() 个
个![]() 销售利润为
销售利润为![]() 元.
元.
(i)求关于![]() 的函数关系式;
的函数关系式;
(ii)结合上述频率分布直方图,以额率估计概率的思想,估计当天利润![]() 不小于650元的概率.
不小于650元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次数学测验共有10道选择题,每道题共有四个选项,且其中只有一个选项是正确的,评分标准规定:每选对1道题得5分,不选或选错得0分,某考试每道都选并能确定其中有6道题能选对,其余4道题无法确定正确选项,但这4道题中有2道能排除两个错误选项,另2题只能排除一个错误选项,于是该生做这4道题时每道题都从不能排除的选项中随机挑选一个选项做答,且各题做答互不影响.
(Ⅰ)求该考生本次测验选择题得50分的概率;
(Ⅱ)求该考生本次测验选择题所得分数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在点P(1,f(1))处的切线方程为y=3x+1,y=f(x)在x=-2处有极值.
(1)求f(x)的解析式.
(2)求y=f(x)在[-3,1]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P–ABCD中,底面ABCD是边长为6的正方形,PD平面ABCD,PD=8.
(1) 求PB与平面ABCD所成角的大小;
(2) 求异面直线PB与DC所成角的大小.
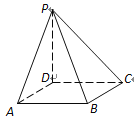
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,点
是菱形,点![]() 在线段PC上,且三棱锥
在线段PC上,且三棱锥![]() 的体积是四棱锥
的体积是四棱锥![]() 的体积的
的体积的![]() ,
,![]() ,
,![]() 平面
平面![]() .
.
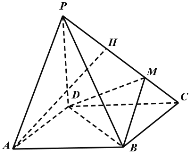
(1)若![]() 是
是![]() 的中点,证明:直线
的中点,证明:直线![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长该地一建设银行统计连续五年的储蓄存款(年底余额)得到下表:
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为便于计算,工作人员将上表的数据进行了处理(令![]()
![]() ),得到下表:
),得到下表:
时间t | 1 | 2 | 3 | 4 | 5 |
储蓄存款z | 0 | 1 | 2 | 3 | 5 |
(1)求z关于t的线性回归方程;
(2)通过(1)中的方程,求出y关于x的回归方程;
(3)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
附:线性回归方程![]() ,其中
,其中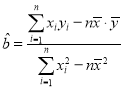 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com