
已知函数f(x)=2sin(2x+φ)(0<φ<2π)的图象过点(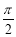 ,-2).
,-2).
(1)求φ的值;
(2)若f( )=
)=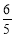 ,-
,-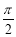 <α<0,求sin(2α-
<α<0,求sin(2α- )的值.
)的值.
(1)φ=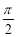 .(2)
.(2) .
.
【解析】
试题分析:(1)因为函数f(x)=2sin(2x+φ)(0<φ<2π)的图象过点(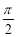 ,-2),所以f(
,-2),所以f(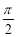 )=2sin(π+φ)=-2,
)=2sin(π+φ)=-2,
即sinφ=1.因为0<φ<2π,所以φ=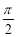 .
.
(2)由(1)得,f(x)=2cos2x.因为f(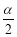 )=
)=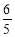 ,所以cosα=
,所以cosα=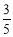 .
.
又因为-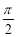 <α<0,所以sinα=-
<α<0,所以sinα=-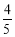 .所以sin2α=2sinαcosα=-
.所以sin2α=2sinαcosα=-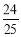 ,cos2α=2cos2α-1=-
,cos2α=2cos2α-1=-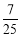 .
.
从而sin(2α-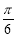 )=sin2αcos
)=sin2αcos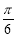 -cos2αsin
-cos2αsin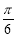 =
= .
.
试题解析:【解析】
(1)因为函数f(x)=2sin(2x+φ)(0<φ<2π)的图象过点(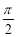 ,-2),
,-2),
所以f(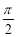 )=2sin(π+φ)=-2,
)=2sin(π+φ)=-2,
即sinφ=1. 4分
因为0<φ<2π,所以φ=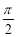 . 6分
. 6分
(2)由(1)得,f(x)=2cos2x. 8分
因为f(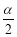 )=
)=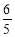 ,所以cosα=
,所以cosα=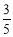 .
.
又因为-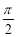 <α<0,所以sinα=-
<α<0,所以sinα=-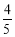 . 10分
. 10分
所以sin2α=2sinαcosα=-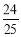 ,cos2α=2cos2α-1=-
,cos2α=2cos2α-1=-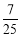 . 12分
. 12分
从而sin(2α-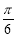 )=sin2αcos
)=sin2αcos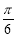 -cos2αsin
-cos2αsin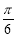 =
= . 14分
. 14分
考点:三角函数解析式,两角差的正弦公式,二倍角公式


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届江苏省高二下学期月考数学试卷(解析版) 题型:解答题
设命题 :函数
:函数 在区间
在区间 上单调递减;命题
上单调递减;命题 :函数
:函数 的最小值不大于0.如果命题
的最小值不大于0.如果命题 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高三9月调研考试文科数学试卷(解析版) 题型:解答题
已知函数f(x)=ax3+|x-a|,a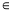 R.
R.
(1)若a=-1,求函数y=f(x) (x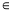 [0,+∞))的图象在x=1处的切线方程;
[0,+∞))的图象在x=1处的切线方程;
(2)若g(x)=x4,试讨论方程f(x)=g(x)的实数解的个数;
(3)当a>0时,若对于任意的x1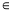 [a,a+2],都存在x2
[a,a+2],都存在x2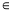 [a+2,+∞),使得f(x1)f(x2)=1024,求满足条件的正整数a的取值的集合.
[a+2,+∞),使得f(x1)f(x2)=1024,求满足条件的正整数a的取值的集合.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高三9月调研考试文科数学试卷(解析版) 题型:填空题
在△ABC中,角A,B,C所对边的长分别为a,b,c.已知a+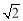 c=2b,sinB=
c=2b,sinB=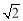 sinC,
sinC,
则cosA= .
查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高三9月调研考试文科数学试卷(解析版) 题型:填空题
某学校高一、高二、高三年级的学生人数之比为4:3:3,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为80的样本,则应从高一年级抽取 名学生.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com