
已知函数f(x)=ax3+|x-a|,a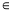 R.
R.
(1)若a=-1,求函数y=f(x) (x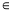 [0,+∞))的图象在x=1处的切线方程;
[0,+∞))的图象在x=1处的切线方程;
(2)若g(x)=x4,试讨论方程f(x)=g(x)的实数解的个数;
(3)当a>0时,若对于任意的x1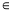 [a,a+2],都存在x2
[a,a+2],都存在x2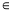 [a+2,+∞),使得f(x1)f(x2)=1024,求满足条件的正整数a的取值的集合.
[a+2,+∞),使得f(x1)f(x2)=1024,求满足条件的正整数a的取值的集合.
(1)2x+y-3=0.(2)当a≥1时,方程f(x)=g(x)有两个不同的解a,-1;当-1<a<1时,方程f(x)=g(x)有三个不同的解a,-1,1;当a≤-1时,方程f(x)=g(x)有两个不同的解a,1.(3){1}.
【解析】
试题分析:(1)当a=-1,x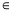 [0,+∞)时,f(x)=-x3+x+1,从而f ′(x)=-3x2+1.当x=1时,f(1)=1,f ′(1)=-2,所以函数y=f(x) (x
[0,+∞)时,f(x)=-x3+x+1,从而f ′(x)=-3x2+1.当x=1时,f(1)=1,f ′(1)=-2,所以函数y=f(x) (x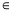 [0,+∞))的图象在x=1处的切线方程为y-1=-2(x-1),即2x+y-3=0.(2)本题第一个难点在于化简方程,提取公因式;第二个难点,在于讨论三个条件关系. f(x)=g(x)即为ax3+|x-a|=x4.所以x4-ax3=|x-a|,从而x3(x-a)=|x-a|.此方程等价于x=a或
[0,+∞))的图象在x=1处的切线方程为y-1=-2(x-1),即2x+y-3=0.(2)本题第一个难点在于化简方程,提取公因式;第二个难点,在于讨论三个条件关系. f(x)=g(x)即为ax3+|x-a|=x4.所以x4-ax3=|x-a|,从而x3(x-a)=|x-a|.此方程等价于x=a或 或
或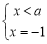 所以当a≥1时,方程f(x)=g(x)有两个不同的解a,-1;当-1<a<1时,方程f(x)=g(x)有三个不同的解a,-1,1;当a≤-1时,方程f(x)=g(x)有两个不同的解a,1.(3)对条件的转化是本题难点,本题从函数值域包含关系出发. 易得函数f(x)在(a,+∞)上是增函数,
所以当a≥1时,方程f(x)=g(x)有两个不同的解a,-1;当-1<a<1时,方程f(x)=g(x)有三个不同的解a,-1,1;当a≤-1时,方程f(x)=g(x)有两个不同的解a,1.(3)对条件的转化是本题难点,本题从函数值域包含关系出发. 易得函数f(x)在(a,+∞)上是增函数,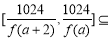 [ f(a+2),+∞).从而
[ f(a+2),+∞).从而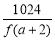 ≥f(a+2).所以f 2(a+2)≤1024,即f(a+2)≤32,也即a(a+2)3+2≤32.因为a>0,显然a=1满足,而a≥2时,均不满足.所以满足条件的正整数a的取值的集合为{1}.
≥f(a+2).所以f 2(a+2)≤1024,即f(a+2)≤32,也即a(a+2)3+2≤32.因为a>0,显然a=1满足,而a≥2时,均不满足.所以满足条件的正整数a的取值的集合为{1}.
试题解析:【解析】
(1)当a=-1,x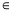 [0,+∞)时,f(x)=-x3+x+1,从而f ′(x)=-3x2+1.
[0,+∞)时,f(x)=-x3+x+1,从而f ′(x)=-3x2+1.
当x=1时,f(1)=1,f ′(1)=-2,
所以函数y=f(x) (x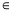 [0,+∞))的图象在x=1处的切线方程为y-1=-2(x-1),
[0,+∞))的图象在x=1处的切线方程为y-1=-2(x-1),
即2x+y-3=0. 3分
(2)f(x)=g(x)即为ax3+|x-a|=x4.
所以x4-ax3=|x-a|,从而x3(x-a)=|x-a|.
此方程等价于x=a或 或
或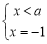 6分
6分
所以当a≥1时,方程f(x)=g(x)有两个不同的解a,-1;
当-1<a<1时,方程f(x)=g(x)有三个不同的解a,-1,1;
当a≤-1时,方程f(x)=g(x)有两个不同的解a,1. 9分
(3)当a>0,x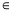 (a,+∞)时,f(x)=ax3+x-a,f ′(x)=3ax2+1>0,
(a,+∞)时,f(x)=ax3+x-a,f ′(x)=3ax2+1>0,
所以函数f(x)在(a,+∞)上是增函数,且f(x)>f(a)=a4>0.
所以当x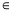 [a,a+2]时,f(x)
[a,a+2]时,f(x) 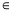 [f(a),f(a+2)],
[f(a),f(a+2)],  ,
,
当x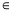 [a+2,+∞)时,f(x)
[a+2,+∞)时,f(x) 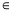 [ f(a+2),+∞). 11分
[ f(a+2),+∞). 11分
因为对任意的x1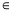 [a,a+2],都存在x2
[a,a+2],都存在x2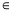 [a+2,+∞),使得f(x1)f(x2)=1024,
[a+2,+∞),使得f(x1)f(x2)=1024,
所以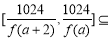 [ f(a+2),+∞). 13分
[ f(a+2),+∞). 13分
从而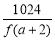 ≥f(a+2).
≥f(a+2).
所以f 2(a+2)≤1024,即f(a+2)≤32,也即a(a+2)3+2≤32.
因为a>0,显然a=1满足,而a≥2时,均不满足.
所以满足条件的正整数a的取值的集合为{1}. 16分
考点:利用导数求切线方程,利用导数求函数值域


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届江苏省高二下学期月考数学试卷(解析版) 题型:解答题
函数 在
在 时取得极小值.
时取得极小值.
(1)求实数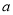 的值;
的值;
(2)是否存在区间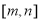 ,使得
,使得 在该区间上的值域为
在该区间上的值域为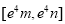 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高三9月调研考试理科数学试卷(解析版) 题型:填空题
记数列{an}的前n项和为Sn.若a1=1,Sn=2(a1+an)(n≥2,n∈N*),则Sn= .
查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高三9月调研考试文科数学试卷(解析版) 题型:解答题
已知函数f(x)=2sin(2x+φ)(0<φ<2π)的图象过点(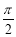 ,-2).
,-2).
(1)求φ的值;
(2)若f( )=
)=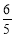 ,-
,-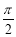 <α<0,求sin(2α-
<α<0,求sin(2α- )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高二下4月月考数学试卷(解析版) 题型:填空题
有在外观上没有区别的5件产品,其中3件合格,2件不合格,从中任意抽检2件,则至少有一件不合格的概率为___________.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高二下学期期中考试理科数学试卷(解析版) 题型:填空题
有A、B、C、D、E五位同学参加比赛,决出了第一到第五的名次。A、B两位学生去问成绩,老师对A说:你的名次不知道,但肯定没得第一名;又对B说:你是第三名.请你分析一下,这五位同学的名次排列的种数为 ;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com