
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)由题意列出2×2列联表,计算观测值K2,对照数表即可得出正确的结论;
(2)根据题意,得出商品和服务都好评的概率,求出X的可能取值,计算对应的概率值,写出期望与方差.
解答 解:(1)由题意可得关于商品和服务评价的2×2列联表为:
| 对服务好评 | 对服务不满意 | 合计 | |
| 对商品好评 | 80 | 40 | 120 |
| 对商品不满意 | 70 | 10 | 80 |
| 合计 | 150 | 50 | 200 |
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | ${(\frac{3}{5})^5}$ | $C_5^1(\frac{2}{5}){(\frac{3}{5})^4}$ | $C_5^2{(\frac{2}{5})^2}{(\frac{3}{5})^3}$ | $C_5^3{(\frac{2}{5})^3}{(\frac{3}{5})^2}$ | $C_5^4{(\frac{2}{5})^4}{(\frac{3}{5})^1}$ | ${(\frac{2}{5})^5}$ |
点评 本题主要考查了统计与概率的相关知识,包括独立性检验、离散型随机变量的分布列以及数学期望和方差的求法问题,也考查了对数据处理能力的应用问题.


科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x<1} | B. | {-1,0,1} | C. | {-1,0} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
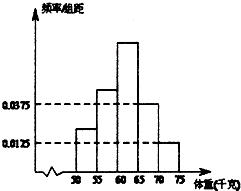 为了解某校高三毕业生报考体育专业学生的体重(单位:千克),将他们的体重数据整理后得到如下频率分布直方图,已知图中从左到右前3个小组的频率之比为1:2:3,其中第二小组的频数为8.
为了解某校高三毕业生报考体育专业学生的体重(单位:千克),将他们的体重数据整理后得到如下频率分布直方图,已知图中从左到右前3个小组的频率之比为1:2:3,其中第二小组的频数为8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
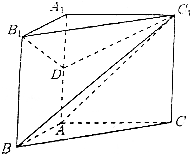 如图,在三棱柱ABC-A1B1C1中.AA1⊥平面ABC,AA1=AC=2AB=2,BC1⊥A1C.
如图,在三棱柱ABC-A1B1C1中.AA1⊥平面ABC,AA1=AC=2AB=2,BC1⊥A1C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
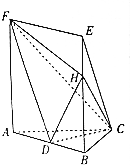 在四棱锥C-ABEF中,底面ABEF是矩形,FA⊥平面ABC,D是棱AB的中点,点H在棱BE上.且AC=BC=$\sqrt{2}$,AB=2,AF=3.
在四棱锥C-ABEF中,底面ABEF是矩形,FA⊥平面ABC,D是棱AB的中点,点H在棱BE上.且AC=BC=$\sqrt{2}$,AB=2,AF=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 休闲方式 性别 | 逛街 | 上网 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.5 | B. | -0.5 | C. | 2.5 | D. | -2.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com