
 如图,在直角坐标系中,以原点O为顶点的两射线l1,l2的夹角为30°,点P先关于射线l1所在直线对称,再关于射线l2所在直线对称后,得到点Q,记为S(P)=Q,并设S0(P)=S(P),Sn(P)=S(Sn-1(P)),n∈N*.若点P为角α的终边上一点(非原点),并记T(P)=sinα,则下列说法错误的是( )
如图,在直角坐标系中,以原点O为顶点的两射线l1,l2的夹角为30°,点P先关于射线l1所在直线对称,再关于射线l2所在直线对称后,得到点Q,记为S(P)=Q,并设S0(P)=S(P),Sn(P)=S(Sn-1(P)),n∈N*.若点P为角α的终边上一点(非原点),并记T(P)=sinα,则下列说法错误的是( )| A. | 对任意的点P,都有T(S6(P))=T(P) | |
| B. | 至少存在4个单位圆上的P,使得T(S3(P))=T(P) | |
| C. | 若点P的坐标为(1,0),则有T(S(P))=$\frac{\sqrt{3}}{2}$ | |
| D. | 对任意的点P,都有T(P)+T(S2(P))+T(S4(P))=0 |
分析 两射线l1,l2的夹角为30°,点P先关于射线l1所在直线对称,再关于射线l2所在直线对称后,得到点Q,则Q点相当于P点绕原点逆时针行旋转了60°,进而得到答案.
解答 解:∵两射线l1,l2的夹角为30°,点P先关于射线l1所在直线对称,再关于射线l2所在直线对称后,得到点Q,
则Q点相当于P点绕原点逆时针行旋转了60°,
故对任意的点P,都有S6(P)=P,故T(S6(P))=T(P),故①正确;
单位圆上只存在两个点(1,0),(-1,0),满足T(S3(P))=T(P),故②错误;
若点P的坐标为(1,0),则有T(S(P))=sin60°=$\frac{\sqrt{3}}{2}$,
对任意的点P,都有T(P)+T(S2(P))+T(S4(P))=sinα+sin(α+120°)+sin(α+240°)=0,
故选:B
点评 本题以命题的真假判断与应用为载体,考查了三角函数的求值,三角函数的恒等变换,难度中档.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题“若 x2-5x+6=0,则x=2”的逆否命题是“若 x≠2,则x2-5x+6≠0” | |
| B. | 命题“角α的终边在第一象限,则α是锐角”的逆命题为真命题 | |
| C. | 已知命题 p和 q,若p∨q 为假命题,则命题 p与q中必一真一假 | |
| D. | 命题“若x>y,则 x>|y|”的逆命题是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
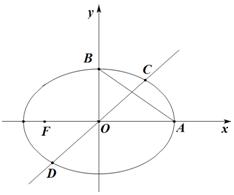 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,点F、A、B分别为E的左焦点、右顶点,上顶点,|AF|=$\sqrt{2}$+1.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,点F、A、B分别为E的左焦点、右顶点,上顶点,|AF|=$\sqrt{2}$+1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$或$\frac{5π}{6}$ | B. | $\frac{π}{4}$或$\frac{5π}{6}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | -$\frac{π}{6}$或-$\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com