
分析 (1)运用求解导数得出f′(x)=$\frac{1}{x}$+2ax,x>0,判断(0,$\frac{\sqrt{2}}{2}$)单调递增,($\frac{\sqrt{2}}{2}$,+∞)单调递减,
得出f(x)极大值=f($\frac{\sqrt{2}}{2}$)=ln$\frac{\sqrt{2}}{2}$+$\frac{1}{2}$,无极小值.
(2)构造g(x)=$\frac{1-x}{a{x}^{2}+1}$,当a>0时g(x)的定义域为R,
g′(x)=$\frac{a{x}^{2}-2ax-1}{(1+a{x}^{2})^{2}}$,g′(x)=$\frac{a{x}^{2}-2ax-1}{(1+a{x}^{2})^{2}}$=0,x1=1$-\sqrt{1+\frac{1}{a}}$,x2=1$+\sqrt{1+\frac{1}{a}}$,
判断得出g(x)在(-∞,x1)(x2,+∞)单调递增,(1,2)单调递减,求解得出极值,得出存在常数M,得出不等式恒成立.
解答 解:(1)函数f(x)=lnx+ax2+1,
f′(x)=$\frac{1}{x}$+2ax,x>0,
当a=-1时,函数f(x)=lnx-x2+1,
f′(x)=$\frac{1}{x}$-2x,x>0,
∴x∈(0,$\frac{\sqrt{2}}{2}$)时,f′(x)>0,
x∈($\frac{\sqrt{2}}{2}$,+∞)时,f′(x)<0;
∴(0,$\frac{\sqrt{2}}{2}$)单调递增,($\frac{\sqrt{2}}{2}$,+∞)单调递减,
∴f(x)极大值=f($\frac{\sqrt{2}}{2}$)=ln$\frac{\sqrt{2}}{2}$+$\frac{1}{2}$,无极小值.
(2)证明:令g(x)=$\frac{1-x}{a{x}^{2}+1}$,当a>0时g(x)的定义域为R,
g′(x)=$\frac{a{x}^{2}-2ax-1}{(1+a{x}^{2})^{2}}$,g′(x)=$\frac{a{x}^{2}-2ax-1}{(1+a{x}^{2})^{2}}$=0,x1=1$-\sqrt{1+\frac{1}{a}}$,x2=1$+\sqrt{1+\frac{1}{a}}$,
g′(x)=$\frac{a{x}^{2}-2ax-1}{(1+a{x}^{2})^{2}}$>0,x1<1$-\sqrt{1+\frac{1}{a}}$,x2>1$+\sqrt{1+\frac{1}{a}}$,
∴g(x)在(-∞,x1)(x2,+∞)单调递增,(1,2)单调递减,
g(1)=0,当x<1时,g(x)>0,
当x<1时,0<g(x)<g(x1)
∴当x>1时,0<g(x)<g(x2)
记M=max||g(x1)|g(x2)|,
a>0时,当λ∈[M,+∞),使得|${\frac{1-x}{f(x)-lnx}}$|≤λ恒成立.
点评 本题考查了导数在解决函数最值,不等式恒成立问题的综合运用,学生的运用算化简能力,分析问题的能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 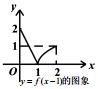 | B. | 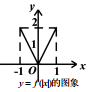 | C. | 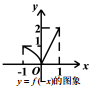 | D. | 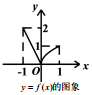 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
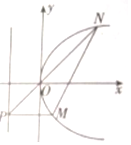 椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2,离心率e=$\frac{1}{2}$,过F2作x轴垂直的直线交椭圆C于A、B两点,△F1AB的面积为3,抛物线E:y2=2px(p>0)以椭圆C的右焦点F2为焦点.
椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2,离心率e=$\frac{1}{2}$,过F2作x轴垂直的直线交椭圆C于A、B两点,△F1AB的面积为3,抛物线E:y2=2px(p>0)以椭圆C的右焦点F2为焦点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在直角坐标系中,以原点O为顶点的两射线l1,l2的夹角为30°,点P先关于射线l1所在直线对称,再关于射线l2所在直线对称后,得到点Q,记为S(P)=Q,并设S0(P)=S(P),Sn(P)=S(Sn-1(P)),n∈N*.若点P为角α的终边上一点(非原点),并记T(P)=sinα,则下列说法错误的是( )
如图,在直角坐标系中,以原点O为顶点的两射线l1,l2的夹角为30°,点P先关于射线l1所在直线对称,再关于射线l2所在直线对称后,得到点Q,记为S(P)=Q,并设S0(P)=S(P),Sn(P)=S(Sn-1(P)),n∈N*.若点P为角α的终边上一点(非原点),并记T(P)=sinα,则下列说法错误的是( )| A. | 对任意的点P,都有T(S6(P))=T(P) | |
| B. | 至少存在4个单位圆上的P,使得T(S3(P))=T(P) | |
| C. | 若点P的坐标为(1,0),则有T(S(P))=$\frac{\sqrt{3}}{2}$ | |
| D. | 对任意的点P,都有T(P)+T(S2(P))+T(S4(P))=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相离 | B. | 相交但直线过圆心 | ||
| C. | 相切 | D. | 相交但直线不过圆心 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
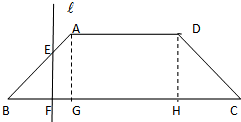 已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.
已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<2} | B. | {x|-3<x<3} | C. | {0,1} | D. | {0,1,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com