
分析 由f(x)=ln(x2-x+1)=0,先求出当x∈(0,$\frac{3}{2}$)时的零点个数,然后利用周期性和奇偶性判断f(x)在区间[0,6]上的零点个数即可.
解答 解:∵f(-x)=-f(x),
∴函数为奇函数,
∴在[0,6]上必有f(0)=0.
当x∈(0,$\frac{3}{2}$)时,由f(x)=ln(x2-x+1)=0得x2-x+1=1,
即x2-x=0.解得x=1.
∵f(x-3)=f(x),
∴函数是周期为3的奇函数,
∴f(0)=f(3)=f(6)=0,此时有3个零点0,3,6.
又f(1)=f(4)=f(-1)=f(2)=f(5)=0,此时有1,2,4,5四个零点.
当x=$\frac{3}{2}$时,f($\frac{3}{2}$)=f($\frac{3}{2}$-3)=f(-$\frac{3}{2}$)=-f($\frac{3}{2}$),
∴f($\frac{3}{2}$)=0,
即f($\frac{3}{2}$)=f($\frac{3}{2}$+3)=f($\frac{9}{2}$)=0,
此时有两个零点$\frac{3}{2}$,$\frac{9}{2}$.
∴共有9个零点.分别为:0,3,6,1,2,4,5,$\frac{3}{2}$,$\frac{9}{2}$.
故答案为:9.
点评 本题主要考查函数零点的判断,利用函数的周期性和奇偶性,分别判断零点个数即可,综合性较强.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在直角坐标系中,以原点O为顶点的两射线l1,l2的夹角为30°,点P先关于射线l1所在直线对称,再关于射线l2所在直线对称后,得到点Q,记为S(P)=Q,并设S0(P)=S(P),Sn(P)=S(Sn-1(P)),n∈N*.若点P为角α的终边上一点(非原点),并记T(P)=sinα,则下列说法错误的是( )
如图,在直角坐标系中,以原点O为顶点的两射线l1,l2的夹角为30°,点P先关于射线l1所在直线对称,再关于射线l2所在直线对称后,得到点Q,记为S(P)=Q,并设S0(P)=S(P),Sn(P)=S(Sn-1(P)),n∈N*.若点P为角α的终边上一点(非原点),并记T(P)=sinα,则下列说法错误的是( )| A. | 对任意的点P,都有T(S6(P))=T(P) | |
| B. | 至少存在4个单位圆上的P,使得T(S3(P))=T(P) | |
| C. | 若点P的坐标为(1,0),则有T(S(P))=$\frac{\sqrt{3}}{2}$ | |
| D. | 对任意的点P,都有T(P)+T(S2(P))+T(S4(P))=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
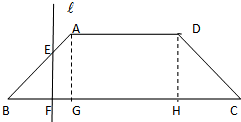 已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.
已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16π | B. | 12π | C. | 4$\sqrt{3}$π | D. | 6π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com